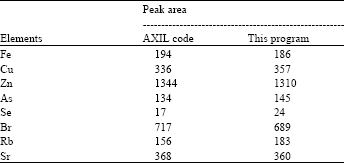
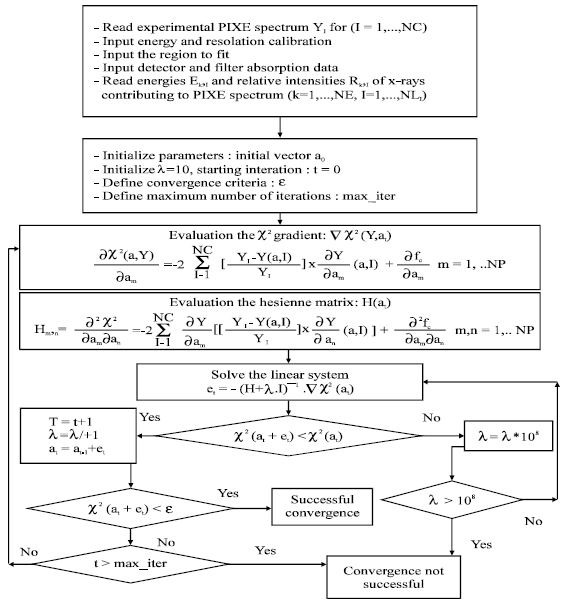
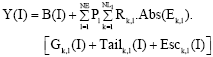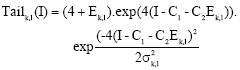Research Article
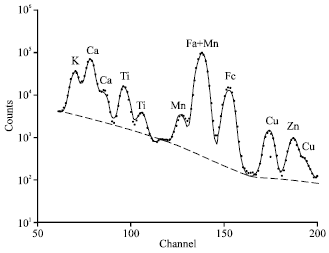
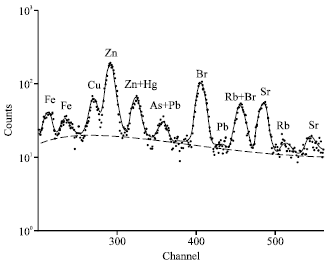
Nonlinear Least-squares Fitting for PIXE Spectra
University of El A�n, El A�n, United Arab Emirates
M.A Benamar
Faculty of Sciences, University of Blida, Blida, Algeria
A. Azbouche
Centre de Recherche Nucleaire dAlger 02, Boulevard Frantz Fanon, B.P. 399 Alger-Gare, Algiers, Algeria
N. Benouali
Draria Nuclear Research Center, Drana, Algeria
S. Tobbeche
Centre de Recherche Nucleaire dAlger 02, Boulevard Frantz Fanon, B.P. 399 Alger-Gare, Algiers, Algeria