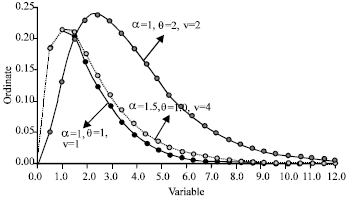
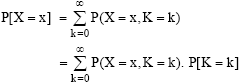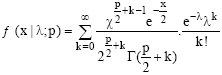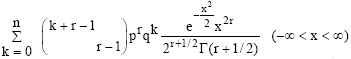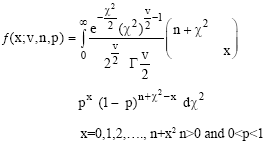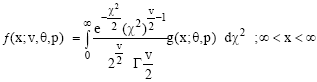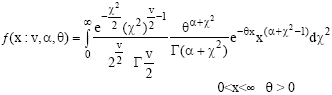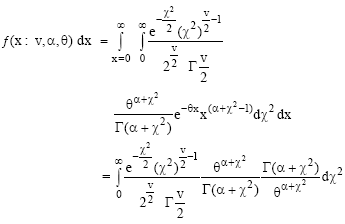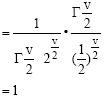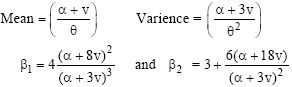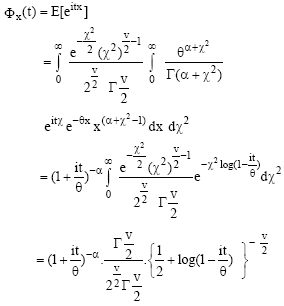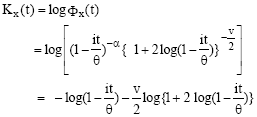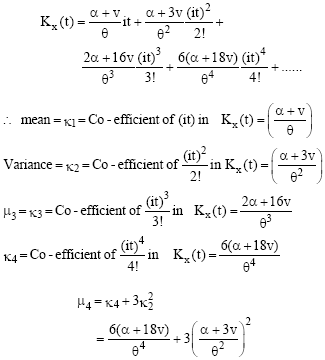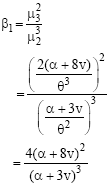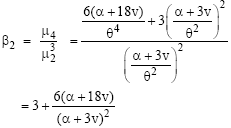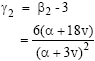Research Article
Chi-square Mixture of Gamma Distribution
Agricultural Statistics Division, Bangladesh Rice Research Institute, Gazipur, Bangladesh
M.K. Roy
Department of Statistics, University of Chittagong, Chittagong, Bangladesh
N. Akhter
Curriculum Development Unit, National Curriculum and Textbook Board, Dhaka, Bangladesh