ABSTRACT
A variable X follows chi square distribution and another variable Y follows gamma distribution, then Z = f(x,y) follows chi square mixture of gamma distribution. In this study, Chi-square mixture of Gamma distribution has been defined and determines mean, variance, skewness and kurtosis of the distribution. This distribution is always positively skewed and leptokurtic for any value of the parameters.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.1632.1635
URL: https://scialert.net/abstract/?doi=jas.2005.1632.1635
INTRODUCTION
A mixture of distributions is a weighted average of probability distribution with positive weights that sum to one. The distributions thus mixed are called the components of the mixture. The weights themselves comprise a probability distribution called the mixing distribution. Because of these weights, a mixture is in particular again a probability distribution. Probability distributions of this type arise when observed phenomena can be the consequence of two or more related, but usually unobserved phenomena, each of which leads to a different probability distribution. Mixtures and related structures often arise in the construction of probabilistic models. Pearson[1] was the first researcher in the field of mixture distributions who considered the mixture of two normal distributions. After the Pearson there was a log gap in the field of mixture distributions. In 1948, Robbins[2] studied some basic properties of mixture distributions. After Robbins, two statisticians Mendenhall and Haider[3] studied on the estimation of parameters of mixed exponentially distributed failure time distributions form censored lifetime data. In the same year, Ashford[4] did another type of study which was different from the study of Mendenhall and Haider[3]. Decay[5] has improved the results of Pearson[1] and Hasselbled[6] studied in grater detail about the finite mixture of distributions.
An example can be stated here that the weights of male population for a particular area follow a normal distribution approximately and the weights of female population for that area follow another normal distribution approximately. Then the probability distribution of the weights of population for that area will be, to the same degree of approximation, a mixture of two, normal distribution. Two separate normal distributions are the components and the mixing distribution is the simple one on the dichotomy male-female population, with the weights given by the relative frequencies of male and female population of that area. Let us consider the following hierarchy,
The marginal density of X is obtained as
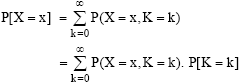 | (1) |
Now since X/(K=k) is χ2p+2k and K is Poisson (λ), the marginal density of X can be obtained as
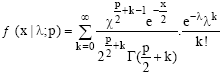 | (2) |
Which is nothing but the non-central chi-square distribution with degrees of freedom p and non-centrality parameter λ. Thus non-central chi-square distribution is considered as a Poisson mixture of chi-square distributions.
PRELIMINARIES
Mixtures mostly occur when the parameter θ of a family of distributions, given by the density function ƒ (x;θ), is itself subjected to the chance variation.
The general formula for the finite mixture is:
| (3) |
and the infinite analogue is
| (4) |
Where, g(θ) is a density function.
Definition 1: Roy et al.[7] defined that a random variable X is said to have a Poisson mixture of distributions, if its density function is given by:
| (5) |
Definition 2: Roy et al.[8] defined that a random variable X is said to have a binomial mixture of distributions Roy et al.[8], if its density function is given by
| (6) |
Where, ƒ (x;θ) is a density function.
Definition 3: Roy et al.[9] defined that a random variable X is said to have a negative binomial mixture of distributions, if its density function is given by:
| (7) |
Where, g(x;r,θ) is a density function.
Definition 4: Roy et al.[10] defined that a random variable X is said to have a negative binomial mixture of normal moment distributions, if its density function is given by:
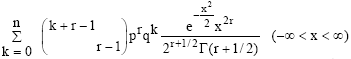 | (8) |
Definition 5: Zaman et al.[11] defined that a random variable X is defined to be a chi-square mixture of binomial distributions with v d.f. and parameters n and p, if its density function is defined by
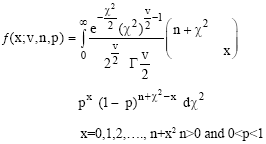 | (9) |
MODEL AND DENSITY APPROXIMATION OF CHI-SQUARE MIXTURED DISTRIBUTION
Definition 6: A random variable X having the density function
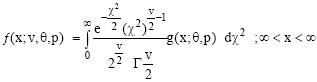 | (10) |
is said to have a chi-square mixtured distributions with n d.f. where g(x;θ,p) is a density function. The name chi-square mixture of distributions is due to the fact that integral values ƒ(x;v,θ,p) in the derived distribution in Eq. 10 is equal to one with weights equal to the ordinates of chi-square distribution having v d.f.
Definition 7: A random variable X is defined to be a Chi-square mixture of Gamma distributions with v d.f. and parameters α and θ, if its density function is defined by
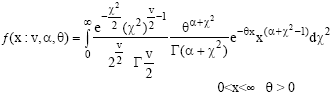 | (11) |
and hence the total probability of this distribution is unity i.e.
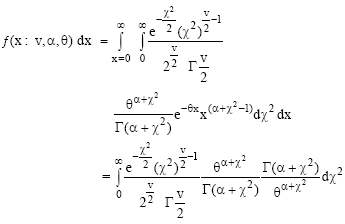 |
 |
RESULTS
The Chi-square mixture of Gamma distribution has been defined in the light of the Chi-square mixtured distributions. The results of the study are presented in the form of theorems.
Theorem 1: If X follows a Chi-square mixture of Gamma distributions with parameters v, α and θ then the characteristics function of the distribution is given by:
and hence
 |
Proof: The characteristics function of the distribution given by:
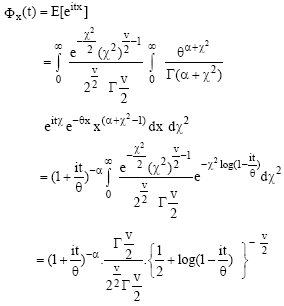 |
on simplifications,
Now the cumulant generating function is:
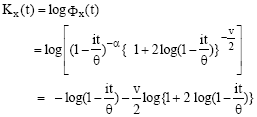 |
on simplifications,
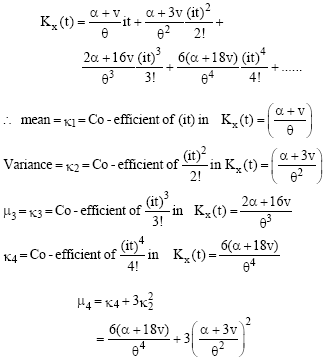 |
Now
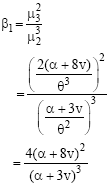 |
So, the coefficient of skewness
and
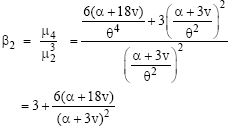 |
So, the coefficient of kurtosis
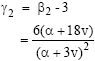 |
Some important properties of the chi-square mixture of Gamma distribution
| • | The mean and variance of the distribution is |
| • | If v=0, then the distribution reduces to gamma distribution |
| • | The distribution is always positively skewed. |
| • | The shape of the distribution is always leptokurtic for any value of the parameter. |
A Computer programme is designed to calculate the ordinates of the distribution for different values of the parameters by Fortran (PROFOR) using numerical integration. The probability curves are drawn in Fig. 1. It which shown that the distribution is always positively skewed and the shape of the distribution is leptokurtic.
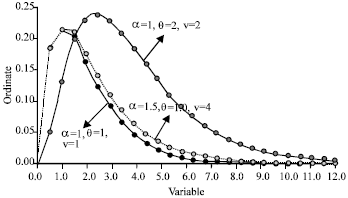 | |
| Fig. 1: | Area curve of the chi-square mixture of Gamma distribution |
REFERENCES
- Decay, F.M., 1964. Modified poisson probability law for a point pattern more than random. Assoc. Am. Geographers Ann., 54: 559-565.
Direct Link








