ABSTRACT
Several at-station analyses have been carried out but none has become known regarding the variation in exponent values of depth, width and velocity for incised channels, which are discussed here. The rate at which the hydraulic geometry parameters change with discharge is quit important to define at-a-station hydraulic geometry relationships. The DEC Project data from Abiaca Creek in USA were used to develop several at-a-station regression relationships for incised channels (CEM Type IV or V). The mean average of these regression equations results in a proposed regression channel geometry equation were W/d = 126.10Q–0.49, d = 0.17Q0.58, W = 20.20 Q0.09 and V = 0.29Q0.33. The exponent of the width is very small, which means the river surface width do not vary significantly with discharge and fairly constant, while the depth, velocity and width depth ratio exponent vary largely with discharge. The results show that the incised channel tends to be narrow and deep compared to equilibrium conditions. The width depth ratio is inversely proportional to the discharge. This result contradicts the results of other investigators for the reason that their workings were done for stable channels.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.1606.1612
URL: https://scialert.net/abstract/?doi=jas.2005.1606.1612
INTRODUCTION
Unlike downstream hydraulic geometry, which deals with spatial variations in channel properties at some reference discharge, at-a-station hydraulic geometry deals with temporal variations in flow variables as discharge fluctuates at a cross-section, unusually for a range discharges up to bankfull.
The hydraulic geometry of a river channel refers to and is described by, the relationships between discharge and certain hydraulic characteristics of the channel, such as width, depth and velocity. Early relationships were developed for canals in India and Pakistan. Regime theory implies that a channel is non-silting and non-scouring[1]. Empirical relationships have been developed by Kennedy[2], Lacey[3] and Blench[4], among many others. Regime theory consists of a set of empirical equations, which can be manipulated to give the width (W), depth (d) and slope (S) of an approximately stable live-bed channel with a cross-sectional form maintained by a local balance between erosion and deposition[5].
The relationships developed by Leopold and Maddock[6] are in the form of power functions, as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| where, | W | = | Channel top width at the water surface (m); |
| d | = | Flow depth (m); | |
| V | = | Flow velocity (m/s); | |
| Q | = | Flow rate (m3/s); | |
| Qss | = | Sediment transport rate and | |
| a, b, c, f, j, k, m, p | = | Empirically-derived coefficients and exponents. |
Numerous researchers have used this approach to describe channel shape and form, to classify rivers and to correlate channel geometry to geomorphologic variables[7]. Richards[8] pointed out that for many rivers, the scatter of points on hydraulic geometry diagrams is often better fit by polynomial relationships (fit to the logarithms of the variables) rather than by linear relationships.
Ackers[9] obtained a constant width/depth ratio for stable laboratory streams, using a small stream for his experimentation; he developed width and depth relationships in terms of discharge. The bed and bank materials used were sand with a median diameter that ranged between 0.16 to 0.34 mm and the discharge values ranged between 0.4 to 5.4 cfs-1. Sediment concentrations up to 400 parts per million (ppm) were observed.
A regime analysis of the data gave the following equations:
| (5) |
| (6) |
| (7) |
The width/depth ratio in (7) is almost a constant and is equal to 12.9.
Schumm[10] studied the effects that the percentage of silt-clay (alluvial material smaller than 0.074 mm) in the banks had on the shape of stream channels. He used a power function to relate the width/depth ratio to the percentage of silt-clay in the channel banks and found that downstream changes in width and depth are greatly influenced by sediment type, specifically that channels containing little silt-clay are relatively wide and shallow. The greater percentage of silt and clay in the perimeter produces a low width/depth ratio cross section and coarser bed and bank material produces a high width/depth ratio cross section. Based on these considerations, Schumm presented empirical relationships for channel width, depth, meander, wavelength and amplitude as functions of the amount of silt and clay and mean annual discharge or mean annual flood. Schumm[11] subdivided channels into three types on the basis of the dominant mode of sediment transport, using the percentage silt-clay (M) in the channel boundary as his criterion:
Bed load channels (M≤5);
Mixed-load channels (5<M<20) and
Suspended-load (or wash load) channels (M≥20).
Bank strength is an important factor controlling a channel cross-sectional shape. Bank strength depends, not only on bank material properties, but also on bank vegetation. This is illustrated by Hey and Thorne[12] who identified four classes of bank vegetation based on type and density of the plants:
Type I: Grassy banks with no trees or shrubs; Type II: 1 to 5% tree/shrub cover; Type III: 5 to 50% tree/shrub cover and Type IV: > 50% tree/shrub cover. |
REGIME
The India Canal data, on which the Kennedy[2] and Lacey[3] regime relationships are based, did not have any record of the rate of bed material transport. But the majority of the India Canal data indicate that conforming channels approximately carry, on the average, bed material load of the order of 500 ppm[13].
Simons and Albertson[14] developed a method for designing uniform alluvial channels. Their design theories, which are recommended include: (1) a modification of the regime theory on India and (2) a modification of the tractive-force theory. The results of their investigation are based on a field study of stable alluvial irrigation channels and other existing alluvial data, which are applicable. The principal finding of their study was that the regime equations, as developed in India[13], are valid for channels having sand beds and slightly cohesive to cohesive banks, which are formed by berming of the suspended material with less than 500 ppm sediment loads over a sustained period of time. The hydraulic geometry relationship for mean depth (m) and surface flow width (m) for sandy banks are:
| (8) |
| (9) |
At-station hydraulic geometry utilizes a range of discharge up to bankfull for single cross-section geometry. Western et al.[15] presented a method for characterizing stream channels using surveyed cross sections, which allows for characterization of longitudinal variability in channel shape, size and slope. They determined a set of parameters to describe the geometry and location of each cross section and then used statistical analysis of the parameters to test specific hypotheses. The parameter set they developed consisted of four variables. The size of the cross section was characterized using bankfull depth (Zbf). The form of the cross section was described using the bankfull width/depth ratio (ω) and a shape parameter (Ψ) defined as the ratio of the bankfull hydraulic mean depth to Zbf. The final parameter described the vertical location of the cross section as the ratio of the deviation of the actual cross-section thalweg elevation from the expected thalweg elevation to Zbf. To obtain the hydraulic characteristics of the cross section as a function of depth, they employed a power function relationship between the width and depth:
| (10) |
where, W* = W/Zbf and Z* = Z/Zbf.
| Table 1: | At-station hydraulic geometry relations[5] |
 | |
| * Symbols: w =aQb, d = cQf, V = kQm, n = tQy, ff = hQP, Q = rQj | |
Ridenour and Giardino[16] observed that finding correlations between geomorphologic variables and channel form is difficult because a stream is such a complex system with many interacting variables; the influence that one variable has on the river system may diminish as other variables change. They used log ratio linear modeling to investigate correlation between at-a-station hydraulic geometry and median grain size (d50) of the bed material and found a lack of correlation between the bed grain size and at-a-station hydraulic geometry but concluded that this is expected in streams where the roughness is dominated by planform characteristics, vegetation elements, macroscale bar features, or bedforms. They suggested that the use of d84 might be more appropriate.
There are numerous relations for at-a-station hydraulic geometry. In each of the selected empirical formulae that are shown in Table 1 none of these equations applicable for incised channel.
INCISED CHANNEL
Watson et al.[17] stated that incised channels are caused by an imbalance between sediment transport and sediment supply to the stream. The resulting bed and bank erosion alter channel morphology and stability. Geomorphological models of incised channel evaluation can provide guidance in the selection of engineering design alternatives for incised channel rehabilitation.
Channel incision, or bed lowering by erosion, results from an imbalance in the power available to move a sediment load and the power needed to move a sediment load. When the sediment transport capacity of a sand bed channel exceeds the sediment supply delivered to the channel, erosion will occur on either the bed or banks or both, depending on the relative erosion resistance of the two[17].
The DEC project seeks to develop and demonstrate a watershed systems approach to address problems associated with watershed instability: erosion, sedimentation, flooding and environmental degradation. The DEC Project is intended to provide sediment, erosion and flood control for 16 watersheds in the Yazoo River Basin in Mississippi. The DEC Project currently includes 33 sites and a total of approximately 64 km of stream. Many of the sites were channelized in the past and are now actively incising.
Watson et al.[18] used conceptual incised Channel Evolution Models (CEM) to study the watershed and channel dynamics and characterized a stable reach of these channels. In each reach of an idealized channel, CEM Types I through V occur in series as shown in Fig. 1. The CEM describes the systematic response of a channel to base-level lowering and encompasses conditions that range from disequilibrium to a new state of dynamic equilibrium.
Watson et al.[18] developed several regression relationships from field stability analysis of a stream based on CEM concepts. Four variables were used in their analysis: drainage area and flow depth, flow width and energy slope at 2-year discharge. The analysis was divided into two parts, the first part for a cross section (CEM Type II or III) and the second part for a cross section (CEM Type IV or V). Descriptions of each type are as follows:
CEM Type I reaches are characterized by a sediment transport capacity that exceeds sediment supply, with little or no sediment stored in the channel bed. CEM Type I reaches are located upstream of the actively degrading reach and have not yet experienced significant bed or bank instabilities. Bank height (h) that is less than the critical bank height (hc) and is a U-shaped cross section.
CEM Type II reaches are located downstream of CEM Type I reaches. CEM Type II reaches are encountered, bed degradation is the dominant process in this type and are characterized by a sediment transport capacity that exceeds the sediment supply. Although the channel is actively degrading the bank heights (h) have not exceeded the critical bank height (hc). Therefore, banks are not geotechnically unstable, but hydraulically are unstable.
CEM Type III reaches are located downstream of CEM Type II and are characterized by a sediment transport capacity that is highly variable with respect to the sediment supply, a bank height (h) that is greater than the critical bank height (hc). As bed degradation continues, the bank heights and angles will continue to increase.
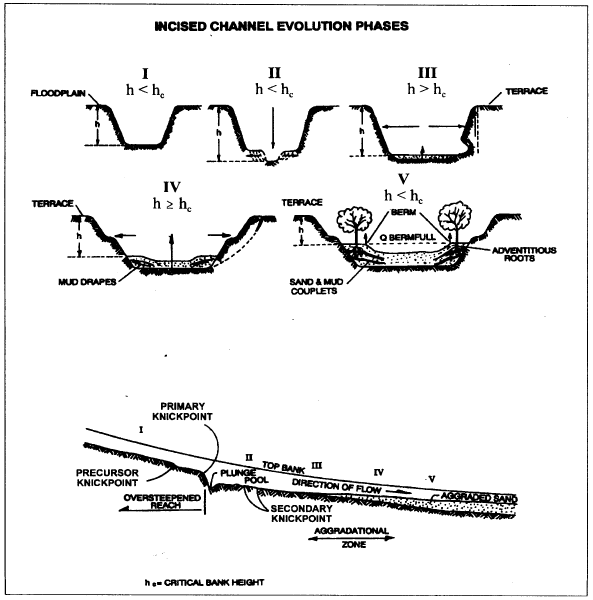 | |
| Fig. 1: | Incised channel evolution sequences[25] |
When the bank heights have exceeded the critical bank height for stability, mass failure (geotechnical instability) begins to occur in this type. The dominant process in the CEM Type III reach is channel widening.
CEM Type IV reaches are located downstream of CEM Type III and represent the first manifestation of the incised channel returning to a new state of dynamic equilibrium. CEM Type IV reaches are characterized by a sediment supply exceeding the sediment transport capacity resulting in aggradation of the channel bed, a bank height that approaches the critical bank height with a rate of bank failure lower than CEM Type III. In the CEM Type IV reaches, geotechnical bank instabilities and channel widening may continue, but at a much reduced rate.
CEM Type V reaches are located downstream of CEM Type IV and are characterized by a dynamic balance between sediment transport capacity and sediment supply, bank heights are generally less than the critical bank and therefore, geotechnical bank instabilities do not exist.
DATA SOURCES
A total of 140 data sets at-a-station were obtained from Abiaca Creek at 7 cross sections DEC Project[18]. Approximate watershed area at the downstream end of Site No. 6 is 257 sq km (99 sq mi).
The at-a-station data contain water discharge (m3s-1), flow width (m), flow velocity and flow depth (m). Data from the Abiaca Creek site No. 6 was used to develop several at-a-station hydraulic geometry equations. Seven cross sections were used to develop the empirical equations. The dependent variables are top width (m), depth (m) and shape factor (Ψ = W/d). Each is a function of an independent variable (Q). The range of flow discharge is between 2.86 to 57.2 m3s-1.
Dependent variables = f (Q) = aQb
RESULTS
The results of this overall non-linear regression analysis are listed in Table 2.
The new empirical channel geometry equations are:
Mean depth (m)-
| (11) |
Mean width (m)-
| (12) |
Mean velocity (m/s)-
| (13) |
| Table 2: | Results of non-linear regression analysis for at-a-station hydraulic geometry |
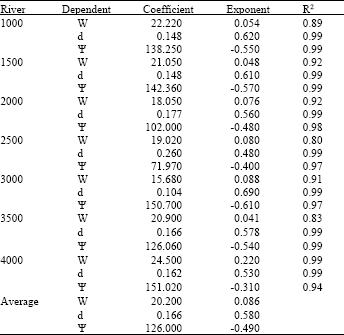 | |
 | |
| Fig. 2: | (a) flow discharge vs. top width, (b) flow discharge vs. flow depth and (c) flow discharge vs. shape factor for Abiaca Creek at station 10+00 ft |
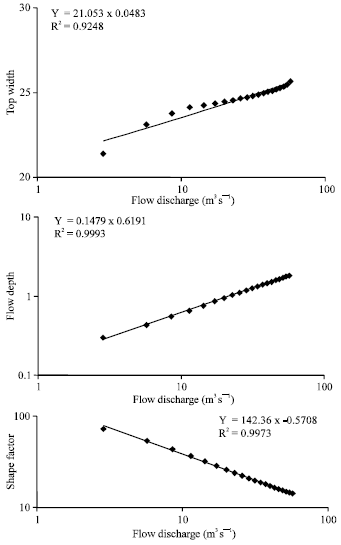 | |
| Fig. 3: | (a) flow discharge vs. top width, (b) flow discharge vs. flow depth and (c) flow discharge vs. shape factor for Abiaca Creek at station 15+00 ft |
Shape factor ψ-
| (14) |
where, Q is in m3/s.
Figure 2 to 4 show the channel geometry equation relationships for the Abiaca Creek at stations 10+00, 15+00 and 20+00 ft.
The width exponent (b) is too small (0.09) that means in incised channel the width nearly constant and independent on flow discharge. The exponent of depth (f) is too high comparing to width exponent, since channel under consideration is incised channel. In incised channel the erosion in the channel bed is more than the boundary, bank strength is an important control of channel cross sectional shape. The definition of volumetric flux requires the product of width depth and velocity to be equal to the discharge.
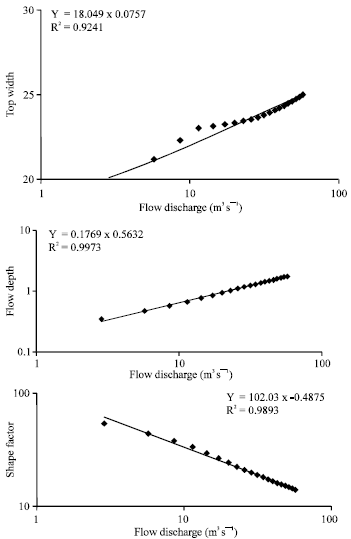 | |
| Fig. 4: | (a) flow discharge vs. top width, (b) flow discharge vs. flow depth and (c) flow discharge vs. shape factor for Abiaca Creek at station 20+00 ft |
Hence, the relationships must satisfy that Q = WdV = 20.2Q0.09x0.17Q0.58x0.29Q0.33, thus the product of coefficients is 20.2x0.17x0.29 = 1 and the sum of exponents is 0.09+0.58x0.33 = 1.
CONCLUSIONS
The variability of at-a station hydraulic geometry inhibits the drawing of simple conclusions. In broad outline, the width exponent (b) appears to be largely a function of channel geometry and therefore boundary composition, while the depth exponent (f) is dependent on cross-section form and partly on sediment transport.
Data from Abiaca Creek were used to develop several at-a-station regression equations. The mean depth, width and shape factor of these proposed regression equations are shown in Eq. 11 to 14. The depth is directly proportional to the flow discharge. It is shown from these equations that the effect of flow discharge on the channel depth is more significant than the effect of flow discharge on the channel width. The regression equations for at a station hydraulic geometry is not generally applicable for large rivers, these equations were relevant for DEC incised channels and similar channels where the width/depth ratio was significantly affected by erosion-resistant clay bank and bed channels.
Typically at-a-station hydraulic geometry relationships for incised channel show the changes in discharge affect primarily the flow depth, velocity and width depth ratio and a lesser extent the flow width. The deepening of the channel is the result from degradation of the channel bed in order to increase the channel capacity. Lowering of bed level has effect of increasing unit stream power and therefore sediment transport.
REFERENCES
- Kennedy, R.G., 1895. The prevention of silting in irrigation canals. Proc. Inst. Civil Eng., 119: 281-290.
CrossRefDirect Link - Lacey, G., 1930. Stable channel in alluvium. Proc. Inst. Civil Eng., 229: 259-292.
CrossRefDirect Link - Richards, K.S., 1973. Hydraulic geometry and channel roughness; a non-linear system. Am. J. Sci., 273: 877-896.
CrossRefDirect Link - Hey, R.D. and C.R. Thorne, 1986. Stable channels with mobile gravel beds. J. Hydraulic Eng. ASCE, 112: 671-689.
CrossRefDirect Link - Western, A.W., B.L. Finlayson, T.A. McMahon and I.C. O'Neill, 1997. A method for characterising longitudinal irregularity in river channels. Geomorphology, 21: 39-51.
CrossRefDirect Link - Ridenour, G.S. and J.R. Giardino, 1995. Logratio linear modelling of hydraulic geometry using indices of flow resistance as covariates. Geomorphology, 14: 65-72.
CrossRefDirect Link - Watson, C.C., D.S. Biedenharn and B.P. Bledsoe, 2002. Use of incised channel evolution models in understanding rehabilitation alternatives. J. Am. Res. Assoc., 38: 151-160.
CrossRefDirect Link - Lewis, L.A., 1969. Some fluvial geomorphic characteristics of the Manati Basin, Puerto Rico. Ann. Assoc. Am. Geographers, 59: 280-293.
CrossRefDirect Link - Wilcock, D.N., 1971. Investigation into the relations between bedload transport and channel shape. Geol. Soc. Am. Bull., 82: 2159-2176.
CrossRefDirect Link - Harvey, A.M., 1975. Some aspects of the relations between channel characteristics and riffle spacing in meandering streams. Am. J. Sci., 275: 470-478.
CrossRefDirect Link








