ABSTRACT
This study was a contribution to the theoretical approach of the wettability notion; it showed that, under no slip boundary condition, the representation of wettability by contact angle was disputed. Two news parameters were proposed to characterize the wettability; a shem of simple experiments was discibed to measure these parameters.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.1602.1605
URL: https://scialert.net/abstract/?doi=jas.2005.1602.1605
INTRODUCTION
The law which governs the behaviour of a Fluid/Fluid (F(1)/F(2)) interface is reletively well known; it is characterized by an « interfacial tension σ » which connectsthe mean H of the interface to the pressure jump accross this interface. Far from any solid wall, this law described by the LAPLACE law[1]: p(1)-p(2) = 2σH (the heigher pressure being always locally on the same side that the center of curvature (Fig. 1).
If now we approach a solide wall S along the (F(1)/F(2)) interface, in a plane perpendiculaire to the wall, we observe that the contact angle θ and (or) the curvature of the interface varies with the nature of the solid surface. To describe this interaction of the wall with the interface, two news surfaces tensions σαs (α = 1.2) are proosed as the necessary energy to increase of one unit the area of the common interface F(α)/S and the only geometric parameter retained is 0; the equilibrium of the trple line (intersection of the three media ) implied then the young relation σ2s-σ1s = σ cos θ (the origine of θ being taken inside the fluid of higher pressure).
The influence of the solid wall introduces also some hystersis phenomenon that we may briefly recall as floow, from the description of the observers: If we modify the constraints on the two fluids, θ can vary between two limit vaules θA and θR (θR < θA) while the contact line is fixed-alternatively, the contact line can move in a directioneither with θ=θA fixed (advancing process).
It is clear that the Young formula cannot take into account the hysteresis phenomena if σ2s, σ1s and σ are constants numbers.
An other remark which is often mentuoned is that the movement of the contact line between two viscous fluids seems to be incompatible with the writting of non sliding condition at the boundary for the two fluids.All the notions evocated above are really important for a lot of engeniering problems(spreading or adhesion of a fluid on asolid surface, assisted recoveryof oil in the soils, lubrications etc…) they are known as the properties of wettability of solid surface, but however, they are not clear anough from the point of the mathematic modeling.
Present objective was then to find out what were the characteristic parameters of a triplet F(1), F(2), S such as:
| • | They could be obtained by experimental measures. |
| • | They allow to compute the shape, the evolution and the stability of a F(1)/F(2) interface in presence of a solid wall S. |
To replyhtis question, we study here the simple problem of a symetrical drop posed (or hanged ) on an horizontal solid support.
Equation of a symetrical drop:
| • | Description-notations |
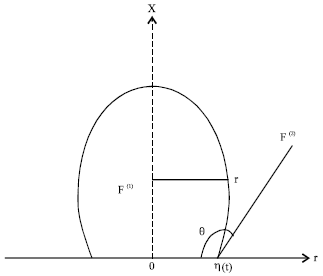 | |
| Fig. 1: | Drop posed on an horizantal plane |
We may represent the boundary of the symetrical drop by Benyettou and Alla[1,2]:
| (1) |
Where, r is the cylindrical radial coordinate and
| • | Necessary condition of spreading of a viscous drop If u is the velocity of a particule of the boundary, then: |
| (2) |
and when x o, the non sliding conditions on the wall implies
but lim ![]()
from there we may conclude
if η(t) > o (Advancing process) then θ(t) =π
if η(t) < o (Receding process) then θ(t) =o
and the paradox of the moving triple line desapears.
| • | Adimentionnal relation for a static drop With the choice of the characteristic lenght |
 | (3) |
[ρ(1)-ρ(2)]g being the difference of the weight by unit of volume of the two fluids, the LAPLACE relation nad the hydrostatic equation[3,4] lead us to the following differencial equation for ![]()
| • |
| • | (4) |
| • |
Where, ![]() (reduced mean curvature of the F(1)/F(2) interface at the contact with the wall),
(reduced mean curvature of the F(1)/F(2) interface at the contact with the wall), ![]() and λ or 0 are unknown pareameters (all relative to the contact) and the
and λ or 0 are unknown pareameters (all relative to the contact) and the ![]() is although given
is although given
However:
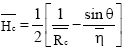 | (5) |
(Rc being the reducted curvature radius of the drop’s profile at the wall ) and (5) gives:
| (6) |
From (5) and (6), ![]() can be eliminated and the foundamental relation (6) leads us to a new interpretation of the hysteresis phenomenon that we describe below as a conjecture.
can be eliminated and the foundamental relation (6) leads us to a new interpretation of the hysteresis phenomenon that we describe below as a conjecture.
A new interpretation of the hysteresis phenomenon conjecture[1]
| • | Remarks |
When the observers say:
dη = o or dη > o or dη < o, it is certaily true because clearly observable
when the observers say :
dθ = o during the advancing or receding process, we may think from (6) that the truth is probably :
| (7) |
Hence we porpose the following conjecture.
| • | Conjecture |
| (8) |
during the advancing process
| (9) |
during the receding process
CA and CR being two constant numbers. When V discreases just after « advancing »
η = constant numbers =ηA and then from (6)
| (10) |
When V̄ increases again just after « Receding ».
η = constant numbers = ηR and then from (6)
| (11) |
| • | Notations for a new analysis and graphic illustration |
| (12) |
Which could contain all the information about the wettability; then:
| (13) |
Whatever, the intial volume may be
In a succession of volume increments from Vo,
we can
To measure η0, η1, …., ηp = ηm
To check that = constant number and in the affirmativ answer,named this number CA;
Then, in a succession of volume decrements from Vm, we can
To check first, that for a while,
and then, from a certain volume Vq, that η begins to decrease in a such way that is a constant number and in the affirmative answer, named this number CR.
In the end, in a last succession of volume increments from Vm
We can close the hysteresis cycle (Fig. 2), checking first that, for a while,
and then, from
η begins again to increase following the rule
| (14) |
We have also to check, that the advantage and the
Receding processes are irreversible while the processes where either ![]() are reversible.
are reversible.
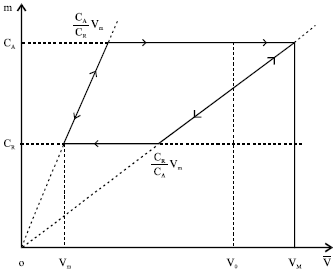 | |
| Fig. 2: | The hysteresis cycle |
ACTUAL STATE OF THE ART
Two short series of experiments seems to confort the conjecture:
| • | η is actually measurable and CA, CR can be determined; | |
| • | We have met a situation without hysteresis; then CA = CR = C; | |
| • | It is scheduled to realize a big number of other experimentations with various partners F(1), F(2), S. | |
| • | Because the hysteresis phenomenon the data of V is generally no sufficient to determine m and the shape φ of the drop ;another element of the hystory of V is necessary. | |
| • | The knowldge of σ, CA and CR seems to be sufficient to determine φ with the data reletive to V. | |
OPEN QUESTIONS
| • | What is the thermodynamic interpretation of CA and CR in terms of energy and dissipation ? |
| • | Is the knowldge of σ, CA and CR for a triple F(1), F(2), S sufficient to compute others situations: Drop on slope, flow in a tube or in a porous media … ? |
| • | What is the interaction between the flow boundary conditions and the conditions at the teiple line? |








