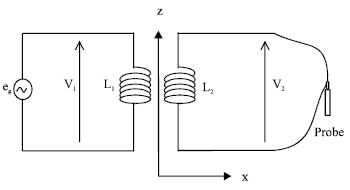
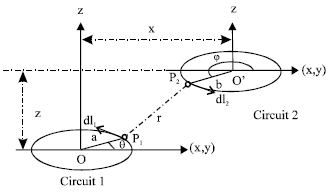
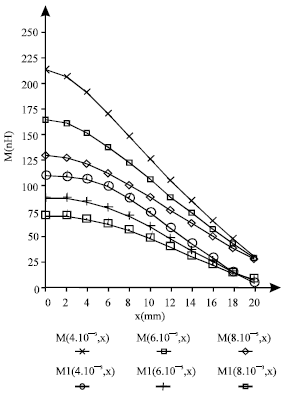
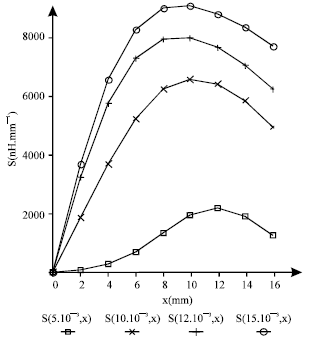
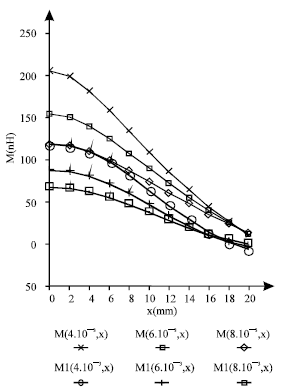
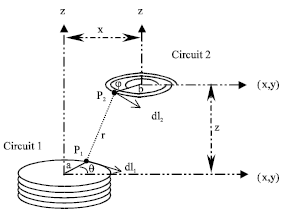
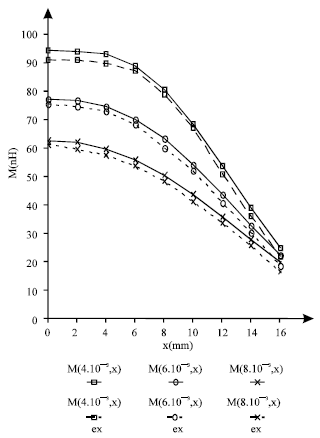
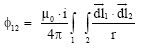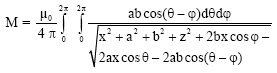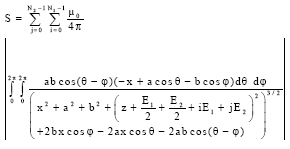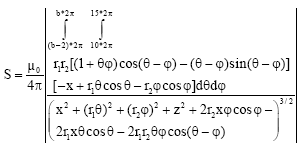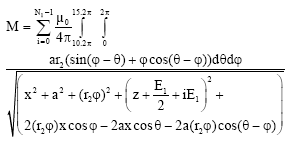Research Article
An Optimal Geometry for Power Energy and Data Transmission in the Inductive Link
National School of Engineering, Laboratory of Electronics and Information Technologies, Tunisia
Hamadi Ghariani
National School of Engineering, Laboratory of Electronics and Information Technologies, Tunisia
Mongi Lahiani
National School of Engineering, Laboratory of Electronics and Information Technologies, Tunisia
Faycak Sellami
National School of Engineering, Laboratory of Electronics and Information Technologies, Tunisia