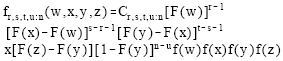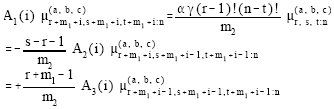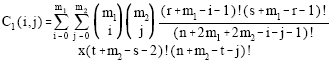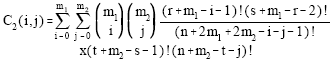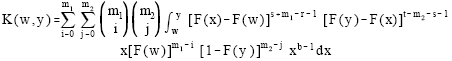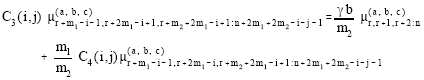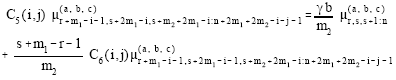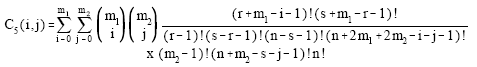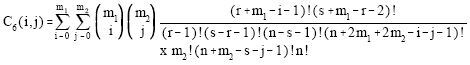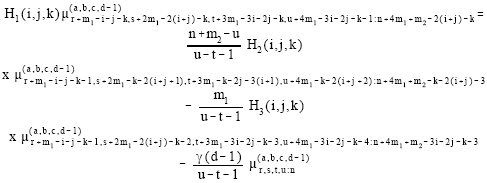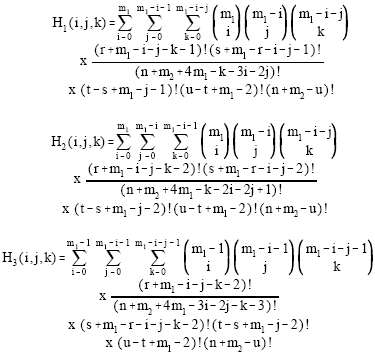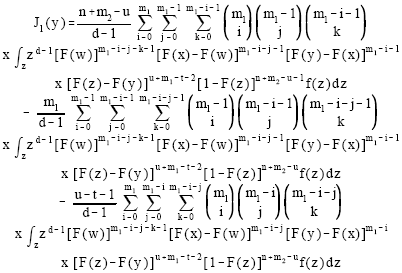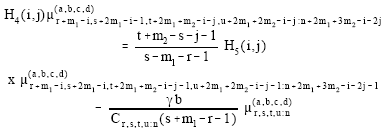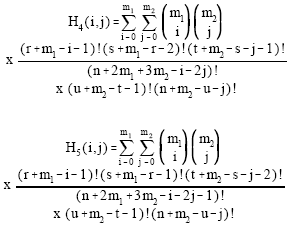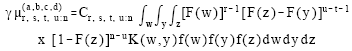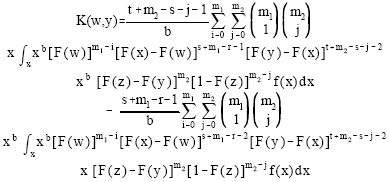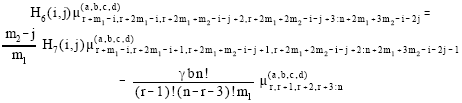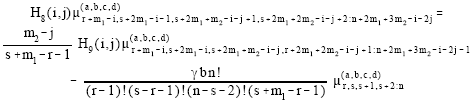Research Article
Further Results on Order Statistics from the Generalized Log Logistic Distribution
Department of Mathematics, Obafemi Awolowo University Ile-lfe, Nigeria
Mathew Oladejo Ojo
Department of Mathematics, Obafemi Awolowo University Ile-lfe, Nigeria









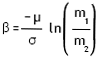 It can be easily shown that the pdf of GLL (m1, m2) becomes
It can be easily shown that the pdf of GLL (m1, m2) becomes