Research Article
A Note on Retailer`s Ordering Policy and Payment Policy under Trade Credit and Cash Discount
Department of Business Administration, Chaoyang University of Technology, Taichung, Taiwan, Republic of China
In practice, the supplier frequently offers the retailer a fixed delay period, that is the trade credit period, in settling the accounts. In real world, the supplier often makes use of this policy to stimulate his/her customer’s demand.
Goyal[1] established a single-item inventory model under permissible delay in payments. Chung[2] developed an alternative approach to determine the economic order quantity under condition of permissible delay in payments. Aggarwal and Jaggi[3] considered the inventory model with an exponential deterioration rate under the condition of permissible delay in payments. Chang et al.[4] extended this issue to varying rates of deterioration. Liao et al.[5] and Sarker et al.[6] investigated this topic in the presence of inflation. Jamal et al.[7] and Chang and Dye[8] extended this issue with allowable shortage. Chang et al.[9] extended this issue with linear trend demand. Chen and Chuang[10] investigated a light buyer’s inventory policy under trade credit by the concept of discounted cash flows. Hwang and Shinn[11] modeled an inventory system for retailer’s pricing and lot sizing policy for exponentially deteriorating products under the condition of permissible delay in payment. Jamal et al.[12] and Sarker et al.[13] addressed the optimal payment time under permissible delay in payment with deterioration. Teng[14] assumed that the selling price was not equal to the purchasing price to modify Goyal’s model[1]. Chung et al.[15] discussed this issue under the assumptions that the selling price is not equal to the purchasing price and different payment rules. Khouja and Mehrez[16] investigated the effect of four different supplier credit policies on the optimal order quantity within the EOQ framework. Shinn and Hwang[17] determined the retailer’s optimal price and order size simultaneously under the condition of order-size-dependent delay in payments. They assumed that the length of the credit period is a function of the retailer’s order size and also the demand rate is a function of the selling price. Chung and Huang[18] examined this problem within the EPQ framework and developed an efficient procedure to determine the retailer’s optimal ordering policy. Huang[19] extended this issue under two levels of trade credit and developed an efficient solution procedure to determine the optimal lot-sizing policy of the retailer.
Therefore, it makes economic sense for the retailer to delay the settlement of the replenishment account up to the last moment of the permissible period allowed by the supplier. From the viewpoint of the supplier, the supplier hopes that the payment is paid from retailer as soon as possible. It can avoid the possibility of resulting in bad debt. So, in most business transactions, the supplier will offer the credit terms mixing cash discount and trade credit to the retailer. The retailer can obtain the cash discount when the payment is paid within cash discount period offered by the supplier. Otherwise, the retailer will pay full payment within the trade credit period. Recently, Huang and Chung[20] extended Goyal’s model[1] to cash discount policy for early payment. Huang[21] relaxed the assumption that the selling price was equal to the purchasing price in Huang and Chung[20].
Model reformulation: For convenience, we adopt the same notation and assumptions as in Huang[21].
| Notation | ||
| D | = | annual demand |
| A | = | cost of placing one order |
| c | = | unit purchasing price per item |
| s | = | unit selling price per item |
| h | = | unit stock holding cost per item per year excluding interest charges |
| Ie | = | interest which can be earned per $ per year |
| Ip | = | interest charges per $ investment in inventory per year |
| r | = | cash discount rate, 0 < r < 1 |
| M1 | = | the period of cash discount |
| M2 | = | the period of trade credit, M1<M2 |
| T | = | the cycle time |
| TVC11(T) | = | the total relevant cost per unit time when payment is paid at time M 1 and T≥M 1 |
| TVC12(T) | = | the total relevant cost per unit time when payment is paid at time M1 and T≤M1 |
| TVC1(T) | = | the total relevant cost per unit time when payment is paid at time M1 and T>0 |
| TVC21(T) | = | the total relevant cost per unit time when payment is paid at time M2 and T≥M2 |
| TVC22(T) | = | the total relevant cost per unit time when payment is paid at time M2 and T≤M2 |
| TVC2(T) | = | the total relevant cost per unit time when payment is paid at time M2 and T>0 |
| TVC(T) | = | the total relevant cost per unit time when T >0 |
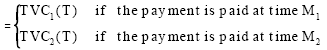 |
| T1* | = | the optimal cycle time of TVC1(T) |
| T2* | = | the optimal cycle time of TVC2(T) |
| T* | = | the optimal cycle time of TVC(T). |
| Assumptions | |
| 1. | Demand rate is known and constant. |
| 2. | Shortages are not allowed. |
| 3. | Time period is infinite. |
| 4. | The lead time is zero. |
| 5. | Ip ≥ Ie and s ≥ c. |
| 6. | During the time the account is not settled, a deposit is made of the unit selling price of generated sales revenue into an interest bearing account. At the end of this period, the retailer pays off all items sold, keeps profits and starts paying for the interest charges on the items in stocks. It is assumed that the interest earned from profits is too small to neglect it. |
| 7. | Supplier offers a cash discount if payment is paid within M1, otherwise the full payment is paid within M2. The account is settled when the payment is paid. |
However, we want to modify the item of interest payable in TVC11(T) in Huang[21]. Since the supplier offers cash discount if payment is paid within M1. Therefore, in this case, the retailer will pay the annual purchasing cost, c(1-r)D, to the supplier. Then, the annual cost of interest charges for the items kept in stock is based on the annual purchasing cost, c(1-r)D. So, we modify the item of interest payable in TVC11(T) in Huang[21]
to
Then, the annual total relevant cost functions is formulated.
| (1) |
| (2) |
| (3) |
and
| (4) |
So,
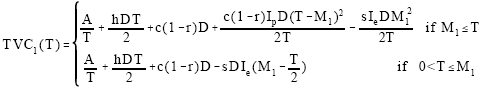 | (5a) (5b) |
and
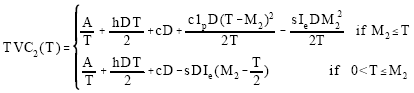 | (6a) |
At T=M1, we find TVC11(M1) = TVC12(M1). Hence TVC1(T) is continuous and well-defined. All TVC11 (T), TVC12(T) and TVC1(T) are defined on T > 0. And at T= M2, we find TVC21(M2)= TVC22 (M2). Hence TVC2 (T) is continuous and well-defined. All TVC21(T), TVC22(T) and TVC2(T) are defined on T>0.
Determination of the optimal cycle time T* and optimal payment policy: From equations (1), (2), (3) and (4) yield
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
and
| (14) |
Equations (10) and (14) imply that all TVC12(T) and TVC22(T) are convex on T>0. However, equation (8) implies that TVC11(T) is convex on T>0 if 2A+DM12[c(1-r)Ip-sIe] > 0. Equation (12) implies that TVC21(T) is convex on T>0 if 2A+DM22(cIp-sIe) > 0.
Let TVC11' (T11*) = TVC12'(T12*) = TVC21' (T21*) = TVC22' (T22*) = 0, we can obtain
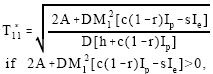 | (15) |
| (16) |
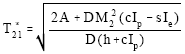 | (17) |
and ![]()
| (18) |
Then, we find T12*= T22*.
Equation (15) implies that the optimal value of T for the case of T≥M1, that is T11*≥M1. We substitute equation (15) into T11*≥M1, then we can obtain the optimal value of T
if and only if -2A+DM12(h+sIe)≤0.
Similarly, equation (16) implies that the optimal value of T for the case of T≤M1, that is T12*≤M1. We substitute equation (16) into T12*≤ M1, then we can obtain the optimal value of T
if and only if -2A+DM12(h+sIe)≥0.
Likewise, equation (17) implies that the optimal value of T for the case of T≥M2, that is T21*≥M2. We substitute equation (17) into T21*≥M2, then we can obtain the optimal value of T
if and only if -2A+DM22(h+sIe) ≤ 0.
Finally, equation (18) implies that the optimal value of T for the case of T≤M2, that is T22*≤M2.
| Table 1: | Comparisons with our solution and Huang’s solution (changing the parameter r) |
 | |
| *PCP(percentage cost penalty)={[ TVCH(T*)- TVCo(T*)]/ TVCo(T*)}*100% | |
We substitute equation (18) into T22*≤M2, then the optimal value of T can obtained
if and only if -2A+DM22(h+sIe)≥ 0.
Furthermore, we let
| (19) |
and
| (20) |
Since M1 < M2, equations (19) and (20) we can get Δ1< Δ2. From above arguments, the optimal cycle time T* and optimal payment policy (M1 or M2) can be obtained as follows:
| Theorem 1 | |
| A: | If Δ1 > 0, then TVC(T*)= min{TVC1(T12*), TVC2(T22*)}. Hence T*= T12*= T22* and optimal payment time is M1 or M2 associated with the least cost. |
| B: | If Δ2 < 0, then TVC(T*)= min{TVC1(T11*), TVC2(T21*)}. Hence T* is T11* or T21*, optimal payment time is M1 or M2 associated with the least cost. |
| C: | If Δ1 < 0 and Δ2 > 0, then TVC(T*)= min{TVC1(T11*), TVC2(T22*)}. Hence T* is T11* or T22*, optimal payment time is M1 or M2 associated with the least cost. |
| D: | If Δ1 = 0 and Δ2 > 0, then TVC(T*)= min{TVC1(M1), TVC2(T22*)}. Hence T* is M1 or T22*, optimal payment time is M1 or M2 associated with the least cost. |
| E: | If Δ1< 0 and Δ2 = 0, then TVC(T*)= min{TVC1(T11*), TVC2(M2)}. Hence T* is T11* or M2, optimal payment time is M1 or M2 associated with the least cost. |
Theorem 1 immediately determines the optimal cycle time T* and optimal payment policy ( M1 or M2) after computing the numbers Δ1 and Δ2. Theorem 1 is really very simple.
A numerical example: To illustrate the results, apply the proposed method to solve the following numerical example to investigate the percentage cost penalty (PCP) between our solution and Huang’s solution[21] changing the parameter of the cash discount rate r. For convenience, the numbers of the parameters are selected randomly.
From Table 1, the optimal cycle time in Huang’s solution[21] will not change when cash discount rate is increasing in this example. Since the optimal cycle time in Huang’s solution[21] in this case is independent of the cash discount rate r. In addition, it is also find the percentage cost penalty is increasing when the cash discount rate is increasing. So, the decision-maker may cause significant errors and penalties using wrong model when the cash discount rate is larger.
The supplier offers the trade credit to stimulate the demand of the retailer. However, the supplier can also use the cash discount policy to attract retailer to pay the full payment of the amount of purchasing cost to shorten the collection period. The credit term that contains cash discount is very realistic in real-life business situations. This note reformulates the retailer’s inventory replenishment model in this situation and modifies Huang’s model[21]. Finally, it is concluded that the decision-maker may cause significant errors and penalties using wrong model when the cash discount rate is larger.
The author would like to thank that this study is partly supported by NSC Taiwan, project No. NSC 92-2213-E-324-014.