ABSTRACT
A method for transmission line embedded cost allocation among transmission transactions based on electricity tracing method is presented. The approach suggested in this paper can allocate transmission embedded cost to both injection points and loading points and hence it is an equitable approach. More importantly the approach can solve the cost allocation problems for bilateral transactions.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2004.427.431
URL: https://scialert.net/abstract/?doi=jas.2004.427.431
INTRODUCTION
The capital investment or embedded costs in transmission is large compared with the operating charges. Considered over the investment recovery period the charges attributable to embedded cost recovery significantly exceed charges attributable to operating costs. The transmission system differs from thermal generating plant in this respect. Although the investment related component dominates in nuclear and hydro generation, unfortunately, costing practices adopted in these cases do not provide any guidance for transmission system embedded cost recovery. In the case of generating plant once the expected annual energy output is estimated the inclusion of a capital related component in the overall charge is a relatively simple matter. Individual transmission lines, however, are variably loaded as system conditions change with time and the extent to which any particular supplier to consumer transmission transaction utilises any particular circuit is difficult to discern. Hence charging for embedded cost recovery is a complex issue.
Not surprisingly, a considerable amount of recent work has been published in the area of embedded cost allocation. Yu and David[1] reported a major study of embedded cost allocation with capacity-use and reliability contribution of transmission lines taken into account. When system loading and transmission line availability probabilities are varying throughout an accounting period, the allocation problem can be approached from the point of view of cooperative game theory[2]. Kovacs and Leverett[3] undertake an evaluation of three load flow based methods for transmission pricing. Though similar to the embedded cost strategies discussed by Yu and David[1] distinguished between incremental and marginal methods in that the former identifies new facilities specifically attributable to specific transmission transactions while the latter is, essentially, a marginal MW-Mile method. Bialek[4] introduced a method of transmission embedded cost allocation based on topological analysis of power flows in a network. The advantages of the method suggested include (i) it is sensitive to the extent of transmission system usage and hence captures the investments in the existing system; (ii) it provides an adequate remuneration of transmission systems and (iii) it is easy to implement. However the problems include (i) the cost is allocated to either generators or loads and hence it is not an equitable approach and (ii) it cannot solve the cost allocation problem for bilateral transaction. The approach suggested in this paper is also based on the electricity tracing method but it solves these two important problems. The cost allocation can be based either on the injection-biased topological model and the loading-biased topological model. The implementation of both models is illustrated through a case study.
Injection-biased topological model: The basic concept of the injection-biased model is to firstly allocate the total transmission embedded cost to various injection points using topological injection distribution factors. For a particular injection point cost allocation, half of the cost is allocated to the party which injects power into the injection point while the other half is allocated to the loads that are supplied by that injection point.
If the gross loading is the sum of actual loading plus allocated transmission losses to the load, the gross power balance equation at node i, when looking at the inflows is
where:
Pig is the gross nodal power flow through node i.
Pgij is the gross line flow in line i-j,
αiu is the set of nodes supplying directly node i
PI i is the injection in node i
Let the actual flow from node j in line ji is Pji and the actual total flow through node j is Pj and assume small transmission loss, then
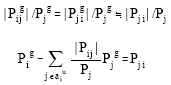 |
| i.e. AuPgross=PI | ||
| Pgross | : | Unknown vector of gross nodal flows |
| PI | : | Vector of nodal injection |
| Au | : | Injection distribution matrix |
The elements of the Au matrix are:
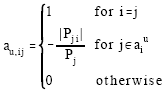 |
As αiu is the set of nodes supplying directly node i, the number of non-zero and non-diagonal elements in row i of the Au matrix represents the number of branches feeding bus i.
Let B u=A u -1 and b u, ik is the element of the matrix B u;
PI k is the real power injection at bus k.
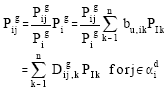 |
where j∈αid, αid is the set of nodes supplied directly from node i. n is the total number of buses in the transmission network. Dgij,k= Pgij bu,ik / Pig is called the topological injection distribution factor. It represents the share of injection of injecting point k in the gross power flow of the line ij as a fraction of the total real power injection of the injecting point k. The share of power injection of injecting point k in the gross power flow of line ij is:
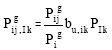 |
Let the total embedded cost of element ij is cij, then the cost of transporting a unit of gross power flow is cij /Pgij,. Suppose the transmission cost allocated to an injection point due to the use of a transmission facility is proportionalto the share of the injection point in the gross power flow of the transmission facility, then the total transmission cost allocated to the injection point k is
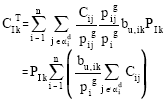 |
This cost is due to the use of the transmission network caused by transportation of power from the injection point k to its related loading points. It is reasonable to let the party which inject power into the point k shares one half of this cost and hence the cost allocated to the party which inject power into the injection point k should be:
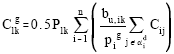 |
Now let the gross power demand at loading bus i (the loading plus the real power loss allocation) is PgLi
The contribution of the injection point k to the gross power demand of the loading bus i is,
All the loads supplied by the injection point k should share the other half of the transmission cost related to the injection point k. The cost allocation should be proportional to the supplying power contribution of the injecting point k to these loading buses. As:
The transmission cost allocation to the loading bus i should be CgLi
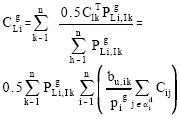 |
Loading-biased topological model: The basic concept of the loading-biased model is to firstly allocate the total transmission embedded cost to various loading points using topological loading distribution factors. For a particular loading point cost allocation, half of the cost is allocated to the party that demand power from the loading point while the other half is allocated to the injection points that supply power to that loading point.
If the net injection is the difference between the actual injection and the allocated transmission loss to the injection, the net power balance equation at node i, when looking at the outflows, is
where:
Pin is the net nodal power flow through node i.
Pnij is the net line flow in line i-j,
αid is the set of nodes supplied directly from node i
PL i is the loading in node i
Let the actual flow from node j in line ji is Pji and the actual total flow through node j is Pj and assume small transmission loss, then
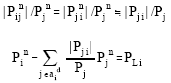 |
| i.e. AdPnet=PL | ||
| Pnet | : | Unknown vector of net nodal flows |
| PL | : | Vector of nodal load demands |
| Ad | : | Demand distribution matrix |
The elements of the Ad matrix are:
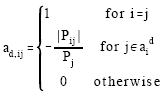 |
As αid is the set of nodes supplied directly from node i, the number of non-zero and non-diagonal elements in row i of the Ad matrix represents the number of branches fed from bus i.
Let B d =A d-1 and b d, ik is the element of the matrix B d;
PL k is the real power loading at bus k.
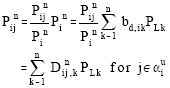 |
where j∈αiu, αiu is the set of nodes supplying directly node i. n is the total number of buses in the transmission network. Dnij,k= Pnij bd,ik/ Pin is called the topological loading distribution factor. It represents the share of demand of loading point k that flow in the line ij as a fraction of the total real power demand of the loading point k. The share of demand at loading point k that flow in line ij is:
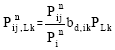 |
Let the total embedded cost of element ij is cij, then the cost of transporting a unit of net power flow is cij / Pnij,. Suppose the transmission cost allocated to a loading point due to the use of a transmission facility is proportional to the share of demand of loading point that flow in the transmission facility, then the total transmission cost allocated to the loading point k is
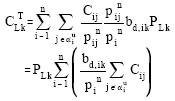 |
This cost is due to the use of the transmission network caused by transportation of power from related injection points to the loading point k. It is reasonable to let the party which demand power at the point k shares one half of this cost and hence the cost allocated to the party which demand power at the loading point k should be:
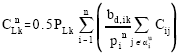 |
Now let the net power injection at bus i (the injection minus the real power loss allocation) is PnIi
The contribution of the net power injection at the injecting point i to the power demand of the loading bus k is,
The other half of the transmission cost related to loading point k should be shared by all the injections supplying the loading point k. The allocation should be proportional to the supplying power contribution to the loading point k from these injection buses. As
The transmission cost allocation to the injection bus i should be CnIi
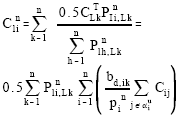 |
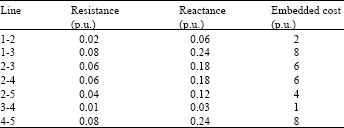
Case study: A simple five-bus network shown in Fig. 1 is used for illustration and the hypothetical parameters of the network including line embedded costs are presented in Table 1. Transaction T1 is the utilities own generation and loads while T2 and T3 are two bilateral transactions. The utility has generator connected to bus 1. At the load buses 4 and 5 250 MW and 300 MW are taken out, respectively. In transaction T2 100 MW is injected at bus 2 and an equal amount is taken out at bus 4 while T3 is such that 200 MW is injected at bus 2 and an equal amount is taken out at bus 3. In all cases transmission losses are accounted for in the operating cost.
Injection-biased topological method: Using the methodology, the injection distribution matrix is:
 |
 |
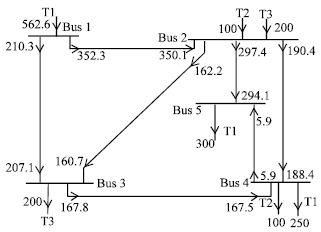 | |
| Fig. 1: | Example for embedded cost study |
| Table 1: | Embedded cost study transmission network data |
 | |
| Table 2: | Transmission charges to injecting and loading buses |
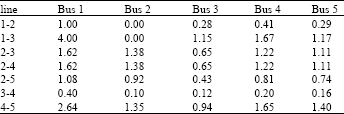 | |
| Table 3: | Transmission transaction total embedded cost allocation |
 | |
| Table 4: | Transmission charges to injecting and loading buses |
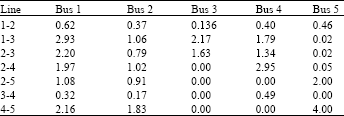 | |
| Table 5: | Transmission transaction total embedded cost allocation |
 | |
Table 2 presents the transmission charges allocated to injecting and loading buses for all the transmission lines while Table 3 presents the transmission cost allocation to different transmission transactions.
Loading-biased topological method: Using the methodology described, the demand distribution matrix is:
 |
| (Pnet)T=(553.3, 643.2, 367.6, 356.0, 300.0) |
Table 4 presents the transmission charges allocated to injecting and loading buses for all the transmission lines while Table 5 presents the transmission cost allocation to different transmission transactions.
Transmission services have to be provided as a separate item in a restructured electricity supply industry. Based on the electricity tracing method, this paper presents a conceptually straightforward mechanism for the allocation of transmission network embedded cost recovery in an equitable manner. The approach suggested can allocate transmission embedded cost to both injecting points and loading points and hence it is an equitable approach. More importantly the approach can solve the cost allocation problems for bilateral transactions. As illustrated through case studies the methodology reflects the quality of transmission service by giving different price signals to transactions. The framework could be used to allocate embedded costs regardless of the number of transactions involved. As every transaction is treated separately by considering only the generation and load associated with the transaction, the methodology is insensitive to the order in which transactions are considered, hence eliminating potential conflicts of interest. Good pricing should achieve equity and efficiency in the utilisation of existing resources and distribute transmission expansion costs in some rational way. It is believed that the methodology proposed in this paper goes some way towards achieving this goal.
REFERENCES
- Yu, C.W. and A.K. David, 1997. Pricing transmission services in the context of industry deregulation. IEEE Trans. Pawer Syst., 12: 503-510.
CrossRef - Yu, C.W. and A.K. David, 1999. An integrated approach to transmission services pricing. IEE Proc. Gener. Transm. Distribution, 146: 255-260.
CrossRef - Kovacs, R.R. and A.L. Leverett, 1994. A load flow based method for calculating embedded, incremental and marginal cost of transmission capacity. IEEE Trans. Power Syst., 9: 272-278.
CrossRef - Bialek, J., 1997. Topological generation and load distribution factors for supplement charge allocation in transmission open access. IEEE Trans. Power Syst., 12: 1185-1193.
CrossRef








