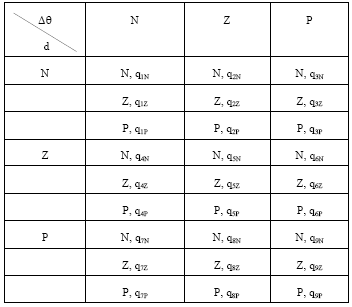
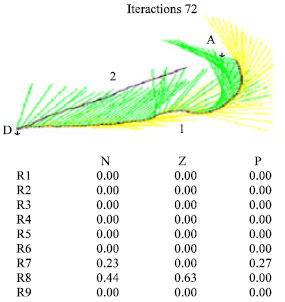
Research Article
Fuzzy Reinforcement Rectilinear Trajectory Learning
Signals Images and Speech Laboratory, Ibn Khaldoun University, B P. 78 C.P. 14000 Tiaret, Algeria
A. Benyettou
Department of Data Processing, University of Sciences and Technology of Oran, B.P. 1505 MNaouer 31000 Oran, Algeria