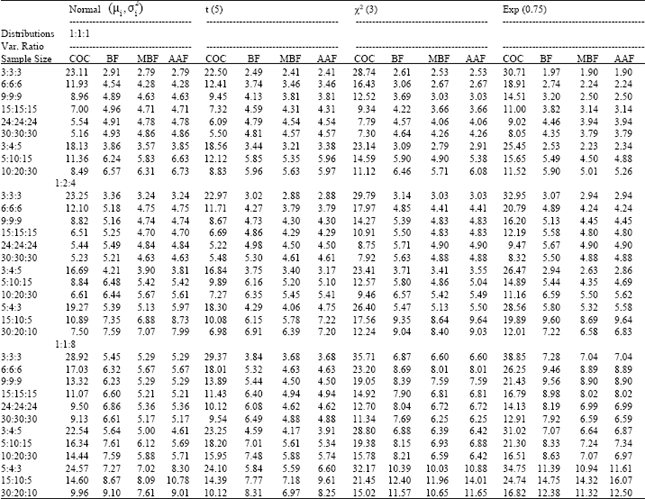
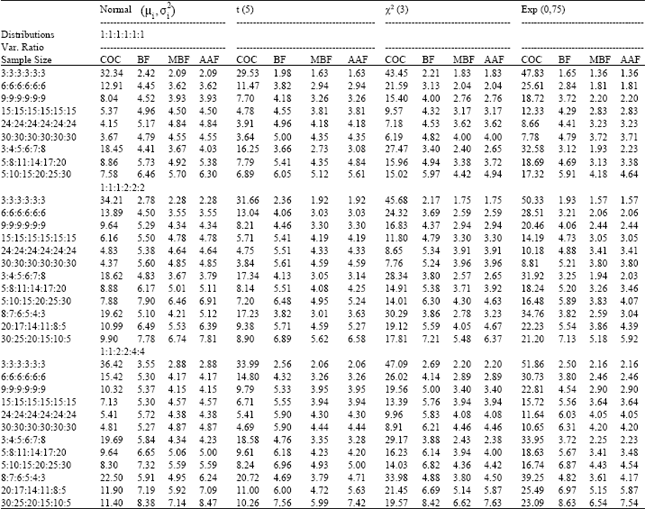
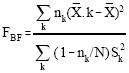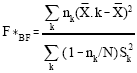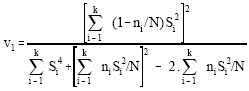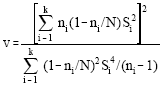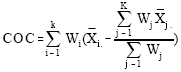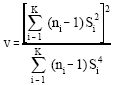Research Article
Evaluation of Four Tests When Normality and Homogeneity of Variance Assumptions are Violated
Biometry and Genetics Department, Faculty of Agriculture, Canakkale Onsekiz Mart University, Canakkale, Turkey
Akin Pala
Department of Animal Science, Faculty of Agriculture, Canakkale Onsekiz Mart University, Canakkale, Turkey









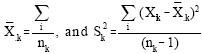 , respectively.
, respectively.