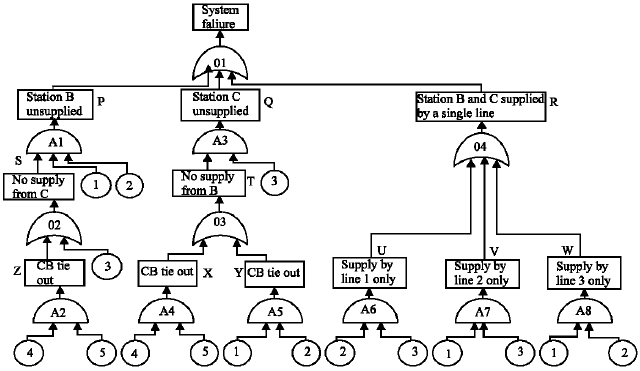
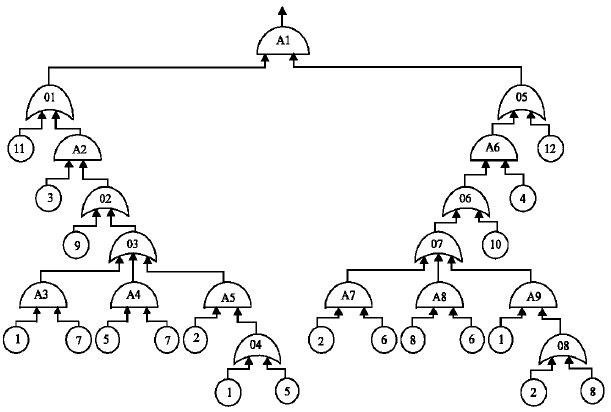
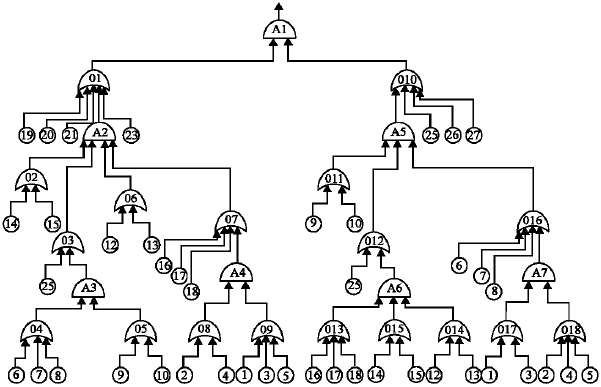
Research Article
Data Structures in Power System Reliability Estimation
Faculty of Engineering, Multimedia University, Jalan Multimedia, 63100, Cyberjaya, Selangor, Malaysia
Morris A.G. Ezra
Faculty of Engineering, Multimedia University, Jalan Multimedia, 63100, Cyberjaya, Selangor, Malaysia