Research Article
Three-Dimensional Calculations of Axial Neutron Flux Distribution in a Material Test Research Reactor
Department of Electrical Engineering, Faculty of Engineering, Mutah University, Mutah, Al-Karak, Jordan
The accurate determination of axial neutron flux distribution in the reactor core is essential for analyzing its irradiation characteristics. It is also required for experimental design, burn-up studies, fuel management and for proper operation of the reactor[1]. In addition, in high power reactors, it is important to determine the axial distribution of neutrons so that unusually high heat generation rate is not produced in localized regions.
The spatial flux distribution in a reactor is a sensitive function of core geometry and materials. It also changes with fuel burn-up and in-core management. For this reason the neutron flux distribution has to be determined frequently[2].
For measurement of neutron flux distribution, the method of multiple foil or wire activation is commonly used[3]. Such an approach is costly as well as time and resources consuming, especially if this process has to be repeated routinely. An alternative way is the use of one or three-dimensional computer codes to calculate the neutron flux distribution. In this case if the reactor is properly modeled and the calculated flux compares favorably with that obtained experimentally, then calculated flux can be used for routine measurements as well as for carrying out various experiments concerning neutron flux distribution.
The above outlined method was used successfully to predict the neutron energy spectrum at different locations in Pakistan Research Reactor-1 (PARR-1), which is a general-purpose material testing reactor[4-10].
This paper focuses on three-dimensional calculation of axial neutron flux distribution in a typical MTR type research reactor as compared to experimental measurement of the flux distribution. It aims at establishing confidence in the calculation methodology to be used for routine determination of flux distribution and in carrying out different studies on the flux distribution.
Theoretical Model: The computer codes WIMS-D/4[11] and CITATION[12] were used for the calculation of the axial neutron flux distribution at three irradiation sites in PARR-1. Brief descriptions of these codes are as follows.
WIMS-D/4: For the generation of group constants, one dimensional transport theory code Winfrith Improved Multi-group Scheme Version-D/4 (WIMS-D/4) has been used. It provides cell-averaged cross-sections and other lattice parameters for overall space dependent reactor calculations. It uses its own 69 energy group library of UK origin that includes 14 fast, 13 resonance and 42 thermal neutron energy groups. The fast neutron energy groups are above 9.118 keV and thermal neutron energy groups are below 4.0 eV.
CITATION: The cross-sections generated by WIMS-D/4 for different regions of the core along with the geometry of the core and surroundings were used as input to the computer code CITATION to calculate neutron flux distribution. The computer code CITATION solves the finite-difference diffusion theory representation of neutron transport theory in one, two and three dimensions. This code can model wide range of geometries such as slab, cylinder, sphere, hexagon and triangle. Depletion problem can also be solved and fuel management calculations for multi-cycle analysis are carried with the help of this computer code. It can also perform calculation of effective delayed neutron fractions and prompt neutron generation time.
Calculations of homogenized cross sections: Group constants for the different parts of the core that is; standard fuel element, control fuel element with absorber (control rod inserted), control fuel element without absorber (control rod withdrawn), control rod, water reflector and graphite reflector materials were calculated using the computer code WIMS-D/4. These constants were computed for 69 energy groups.
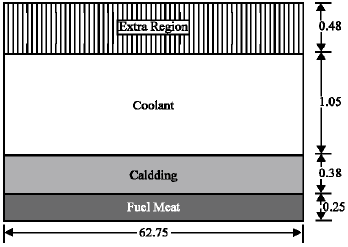 | |
| Fig. 1: | Unit-cell for generation of group constants. All dimensions are in mm |
For generating the group constants for the standard fuel element, the fuel cell was divided into four regions. The water gap between two fuel elements, in the direction normal to the fuel meat and end portion of the fuel elements, were included in the fourth region to have true one dimensional slab representation of infinite lattice. Figure 1 shows the four-region of the cell, which was used for generation of group constants using the SLAB geometry option of WIMS-D/4. Since the cell was symmetric about the center-line, only half of the cell was analyzed. Same methodology was used to generate group constants for control fuel element with and without absorber material. For the other reactor materials like graphite and light water, an extended fuel cell was used. This included one fuel cell surrounded by 10 cm water on both sides to provide a source for the fission neutrons.
Group constants for the reflector material and fuel cell were separated using the REGION card option in WIMS-D/4 code.
Three dimensional diffusion calculation: To obtain the axial neutron flux distribution at the selected sites, the three–dimensional computer code CITATION was used. Calculations were carried out using 69 energy group cross sections generated above. The core configuration considered in this work is the equilibrium core shown in Fig. 2, which was also the configuration during the experimental work. Actual dimensions of the core were used to describe the core in three-dimensions. Moreover the control rods were modeled such that they were inserted to the same level as that when the experiment was performed.
Experimental work: The method of multiple foil activation was selected for the measurement of axial flux distribution. The principal advantages of the use of activation foils are their relative cheapness, small size, insensitivity to gamma rays, independence of electrical connections, minimum perturbation to flux and adaptability to different environments.
 | |
| Fig. 2: | Core configuration used in calculations and experimental work |
Gold foils were placed on Perspex stringers and were irradiated at positions C-4, C-7 and D-3 in the core configuration shown in Fig. 2. The reactor was operated at 100 W for 30 min.
After irradiations and a suitable cooling time the activity of 198Au in each foil, was counted with a PC based and calibrated HPGe detectors. The energy calibration was performed using a standard 152Eu radiation source, which emits many gamma rays. The intensity calibration of the HPGE systems was performed by measuring one of the foils using β - γ coincidence system. The saturation activity Asat was obtained using the formula[13]:
| where | ||
| Nc | = | number of counts registered during a time tc, |
| λ | = | decay constant of 198Au, |
| η | = | Detection efficiency of the measurement system, |
| M | = | mass of gold foil, |
| ti | = | irradiation time, |
| tw | = | cooling time after the end of irradiation, |
The experimentally measured results are given in Table 1 and are plotted in Fig. 3-5. The maximum expected error in the results is less than 2%. The solid lines in these figures represent 4th order polynomial fit to the measured data.
It is clear from Fig. 3-5 that the axial neutron flux is not uniform. These distributions are also not exactly sine shaped. At all the sites, studied in this work, it is noted that the peaks are shifted towards the lower half of the core. This shift can be attributed to the presence of control rods, which were withdrawn to 65% out position when the foils were being irradiated. The presence of control rods in the upper half of the core has the effect of strong absorption of neutrons. Hence, the concentration of neutrons will be more in the lower half of the core. The flux distribution at site D-3 is highly skewed. This is due to the reason that the site is outside the core and is reflected from three sides with graphite. Thus, the presence of the control rod at position D-5 will have a more pronounced effect on the flux distributions at site D-3.
The theoretically calculated results are shown as dotted lines in Fig. 3-5.
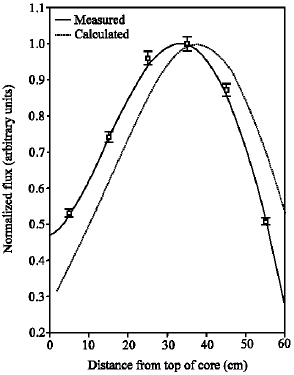 | |
| Fig. 3: | Measured and calculated axial flux distribution at location C-4 of PARR-1 |
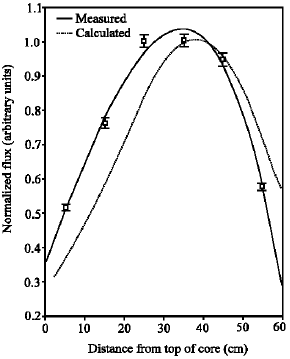 | |
| Fig. 4: | Measured and calculated axial flux distribution at location C-7 of PARR-1 |
It is clear from these figures that both the experimentally measured and the theoretically calculated flux distributions agree on the general shape of the distribution but the peaks do not coincide. Despite the fact that the core was modeled in three dimensions and control rods were placed at the same locations as at the time of the experiment, this discrepancy between the measured and calculated results emphasizes the strong sensitivity of the flux distribution to many parameters.
| Table 1: | Saturated activities of gold foils used in measurement of the axial flux distribution |
 | |
| * Distance measured from top of core | |
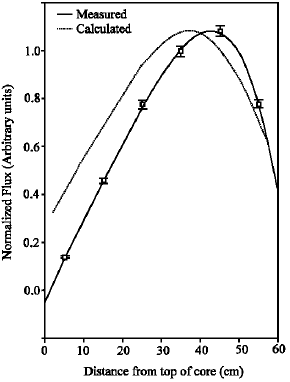 | |
| Fig. 5: | Measured and calculated axial flux distribution at location D-3 of PARR-1 |
This discrepancy can be attributed to a number of reasons. One of these reasons is the degree of burn-up in the fuel[2]. It was assumed in the calculations that all the fuel is fresh, whereas in real case all fuel elements have undergone a certain degree of burn-up. Another reason is the thickness of top and bottom reflectors[14]. Since the actual dimensions of water reflectors around the core are very large (in meters), it was not feasible to use the actual dimensions in the model. For this reason, the CITATION code was run many times with different reflector thickness and after each run the flux distribution outside the core was plotted. This process was repeated until the change in the flux distribution became negligible. One more reason is the presence of instrumentation tubes, which were not accounted for in the calculations. The presence of these tubes allows neutrons to stream through them and hence affects the flux distribution in and around these tubes[15]. It can also be noted that calculated flux distributions at sites C-4 and C-7 are shifted towards the bottom of the core as compared to the measured flux. On the other hand the calculated distribution at site D-3 is shifted towards the top of the core as compared to the measured flux. This is mainly due to the presence of graphite reflectors around site D-3, which can produce this shift when modeled in CITATION[3].
Three-dimensional calculations of the axial flux distribution at a number of irradiation sites in the core of PARR-1 were performed. This was achieved through the use of the transport theory code WIMS-D/4 for preparation of homogenized cross sections and the three-dimensional use of the diffusion theory code CITATION for core analysis calculations.
The good agreement between theoretically calculated flux distribution and experimentally measured flux, using multiple foil activation, gives the calculation methodology used in this work the confidence to be used for routine evaluation of the axial flux distribution, in addition to its use for other types of calculations regarding the neutron flux distribution.