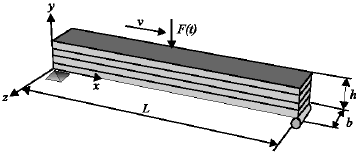
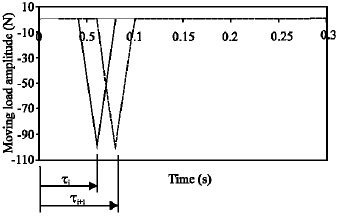
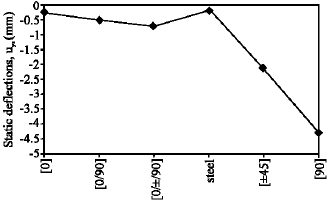
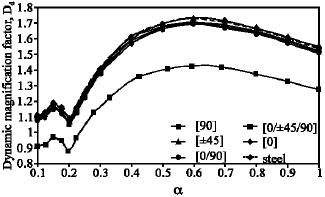
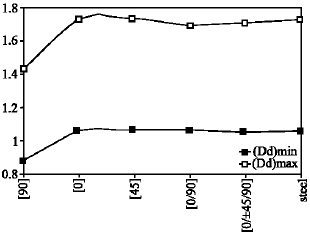
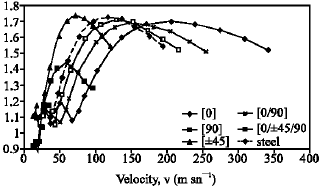
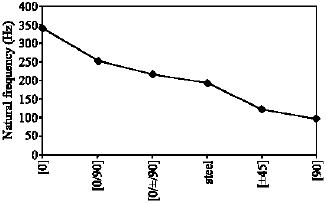
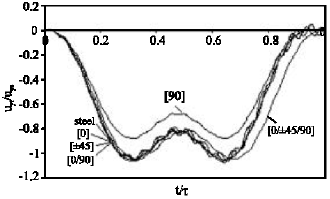
Research Article
Dynamic Behavior of Laminated Composite Beams Subjected to a Moving Load
Mechanical Engineering Department, Dokuz Eylul University, Bornova, Izmir, Turkey
Zeki Kiral
Mechanical Engineering Department, Dokuz Eylul University, Bornova, Izmir, Turkey
Buket Okutan Baba
Mechanical Engineering Department, Cumhuriyet University, Sivas, Turkey