ABSTRACT
In this paper an attempt has been made to develop an absorber for small-size absorption systems. A mathematical model and a computer code for evaluating the theoretical performance of such absorber were developed. This model and code take into account the essential parameters such as solution inlet and outlet conditions, cooling water inlet conditions and absorber geometry. Variation of solution temperature and concentration, cooling water temperature, absorption rate and heat duty across the absorber were presented graphically. Compared to the conventional absorber design, this absorber is expected to attain higher heat and mass transfer coefficients and wetting area and hence a better performance and a reduction in absorber size.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2003.305.316
URL: https://scialert.net/abstract/?doi=jas.2003.305.316
INTRODUCTION
Absorption machines have gained increased interest in the recent years. One of the disadvantages of such machine is its large size components especially the absorber which is the most critical component, and its characteristics have significant effect on overall system efficiency. Reduction of the absorber size needs a well investigation of the absorption process inside the absorber. In this aspect, many research have been theoretically conducted (Andberg and Vliet (1987), Jeong and Garimella (2002)) and many experiments has been carried out (Cosenza and Vliet (1990), Hoffmann (1996), Deng and Ma (1999)). Even though an improvement of absorber efficiency, by the development of tubes having higher efficiency and supply of surfactants, was reported (Yoon and Kim (2002), Beutler et al. (1996)), but this machines still facing difficulties to be adopted as a viable residential absorption system. Recently, Garimella (2000) presented and analyzed a miniaturization technology for absorption heat and mass transfer component. He preliminary modeled it for NH3-H2O system and concluded that such concept holds to the potential for the development of extremely small absorption system components. In this paper, the same concept was considered for LiBr-H2O absorbers with different modeling approach, design and simulation.
A full detailed description of the concept can be found in Garimella (2000) and briefly as follows: Short lengths of small diameter tubes are placed in square array to form one row, Figure (1.a). The second row is placed above the first row in a transverse orientation perpendicular to the tubes in the first row, Figure (1.b). A complete absorber then can be built in the same manner, Figure (1.c). Cooling water flows from bottom to the top through all the rows in series form or parallel through the rows of one pass and then in series through all passes. Strong solution enters from the top while the vapor enters, countercurrent to the solution, from the bottom.
 | |
| Fig. 1: | Schematic of the concept: (a) one row (b) two rows and (c) complete absorber |
Modeling and simulation
A mathematical model and computer code were developed to develop and simulate such absorber or simulate an already existing absorber. In this model, the solution film flow along one half of the tube is modeled as that along a vertical cooled wall with a length of half tube circumference, which is a model suggested by Wassenaar (1995). A schematic representation of the model is shown in Figure (2). Equations of momentum, energy and diffusion of mass and their specific boundary conditions for this situation are represented in four dimensionless combined ordinary differential equations as follows:
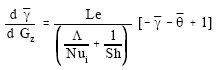 | (1) |
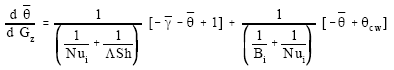 | (2) |
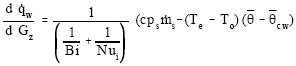 | (3) |
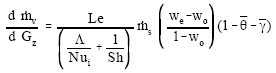 | (4) |
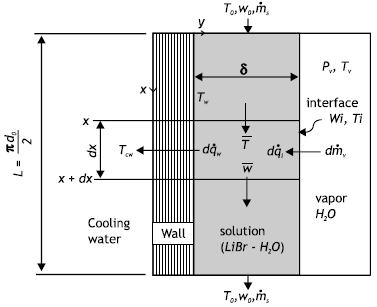 | |
| Fig. 2: | Schematic of the model |
These equations describe the average mass fraction of water in the solution ![]() , the average solution temperature
, the average solution temperature ![]() the heat transferred to the cooling medium across the plate wall per unit width
the heat transferred to the cooling medium across the plate wall per unit width ![]() and the mass transfer of the water vapor to the film per unit width
and the mass transfer of the water vapor to the film per unit width ![]() in one infinitesimal part of the film with length
in one infinitesimal part of the film with length ![]() as shown in Figure (2). A good estimate for the transfer numbers defined in Equations (1-4) are, Wassenaar (1995):
as shown in Figure (2). A good estimate for the transfer numbers defined in Equations (1-4) are, Wassenaar (1995):
| (5a) |
| (5b) |
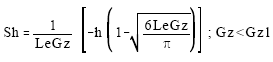 | (5c) |
| (5d) |
| (5e) |
Then, these equations are solved numerically for a unit width of the plate, Khalid and Ali (2001), to give the final form as follows:
| (6) |
| (7) |
| (8) |
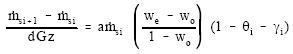 | (9) |
where
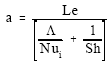 | (10a) |
 | (10b) |
 | (10c) |
Absorber design and simulation
The mathematical model developed in the preceding section can be adopted to design an absorber and simulate an already existing one. In this section absorber design and simulation are presented, respectively. Utilization of the developed mathematical model to design an absorber of such type for specific evaporator cooling capacity, the following design conditions should be given:
| • | Evaporator load QE |
| • | System pressure P |
| • | Solution inlet concentration ξs,i |
| • | Solution inlet temperature Ts,i |
| • | Solution outlet concentration ξs,o |
| • | Solution outlet temperature Ts,o |
| • | Cooling water inlet temperature Tc,i |
From the evaporator load and system pressure and using steam tables, vapor flow rate can be calculated. Then, equating this amount of vapor to the vapor to be absorbed inside the absorber ![]() , the solution flow rate inlet to the absorber
, the solution flow rate inlet to the absorber ![]() and solution outlet flow rate can be calculated as follows:
and solution outlet flow rate can be calculated as follows:
| (11) |
| (12) |
Substituting Equation (11) into Equation (12) yields:
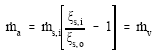 | (13) |
As first step, general absorber geometry to meat the evaporator load is to be selected:
| • | Tube outside diameter (do). |
| • | Tube inside diameter (di). |
| • | Tube length (L). |
| • | Number of tubes per row (NT/R). |
| • | Number of rows per pass (NR/P). |
| • | Number of passes (NP). |
The algorithm for the solution of equations has constructed in C-Language. The flow diagram shown in Figure (3) describes the sequence of various operations. To avoid confusion, the following abbreviations were used for cooling water routine through rows, passes, and the whole absorber as shown in Figure (4).
 | |
| Fig. 3: | Cooling water routine through (a) row, (b) pass and (c) absorber. |
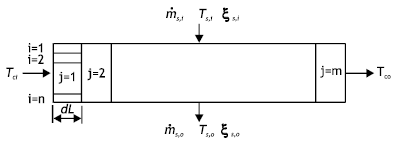 | |
| Fig. 4: | Schematic of one horizontal tube |
| : | Row inlet cooling water temperature, | |
| : | Row outlet cooling water temperature, | |
| : | Pass inlet cooling water temperature, | |
| : | Pass outlet cooling water temperature, | |
| : | Absorber inlet water temperature, | |
| : | Absorber outlet water temperature. |
From the above abbreviations it can be seen that
| (14) |
| 1. | First of all, the necessary parameters and fluid properties are set. | ||||||
| 2. | As simulation of one tube represents all the tubes in the same row, one tube is divided along the length into m sections (starting from the inlet) each of length (dL = L/m). Half circumference of the tube is divided into n equal parts as shown in Figure (4). | ||||||
| 3. | Starting from the most upper row of the most upper pass and at a particular section, the inlet conditions are established on the basis of input parameters such as mass flow rate per unit length per one side of the tube, | ||||||
| 4. | The absorber cooling water outlet temperature, | ||||||
| 5. | Under the input conditions to the tube, Equations (6-9) can be applied to the first part (i = 1) of the first section (j = 1). The inputs start with
| ||||||
| 6. | Solution outlet temperature and concentration for each section is calculated as follows:
| ||||||
| 7. | Steps (5) and (6) are repeated for (j = 2, 3,…, m) with a new cooling water temperature,
| ||||||
| 8. | Heat transfer to the cooling water from the row,
| ||||||
| 9. | Solution temperature and concentration leaving the tube (the row) are computed by taking the average temperature and concentration over all sections (j=1,2,…m). | ||||||
| 10. | Steps (5-9) are repeated for the next rows (Ro = 2, 3,… NR/P) with the above row outlet conditions are used as inputs to the next row until the last row in the pass is reached. | ||||||
| 11. | Pass cooling water outlet temperature is computed by taking the average cooling water outlet temperature over all the rows of the pass. At this stage, if the difference between pass average outlet temperature and the assumed one is greater than a predetermined value,ξ1, the cycle is repeated with reducing the previously assumed | ||||||
| 12. | When the convergence for the upper pass is reached, the whole sequence of operation proceeds to the next pass with pass cooling water outlet temperature is set equal to the upper pass inlet temperature. | ||||||
| 13. | Steps (5-12) are repeated until the last pass is reached. At this stage, absorber cooling water inlet temperature, | ||||||
| 14. | Finally, conditions of the solution leaving the absorber (leaving the last row), | ||||||
| 15. | When the resulted outlet conditions are the same as the design ones the whole results are given and the program terminated. |
This model and computer code was used to develop and simulate an absorber with the design conditions shown in Table (1.a). The absorber geometry selected by the code was shown in Table (1.b) whereas the absorber simulated performance is presented graphically in Figure (5-8).
| Table 1: | (a) design conditions and (b) selected absorber geometry |
 | |
Results and discussion:
Figure (5) shows the variation of solution and cooling water temperatures across the absorber and the corresponding solution concentration is shown in Figure (6).
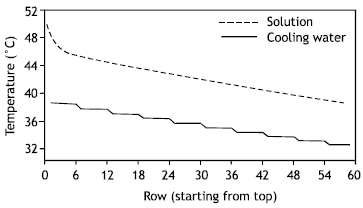 | |
| Fig. 5: | Variation of solution and cooling water temperature across absorber rows |
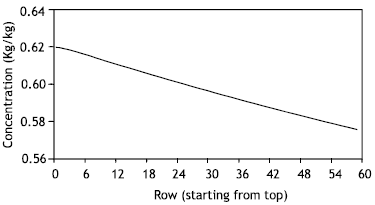 | |
| Fig. 6: | Variation of solution concentration across absorber rows |
 | |
| Fig. 7: | Variation of absorption rate and across absorber rows |
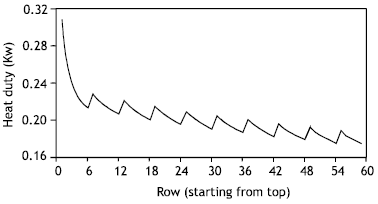 | |
| Fig. 8: | Variation of heat duty across absorber rows |
It can be seen that the solution temperature at the top of the absorber drops significantly as the solution is closed to saturation state, therefore absorption is very small and the cooling water duty is the sensible heat of solution. After this, absorption increases and solution temperature changes tend to stabilize. The cooling water temperature increases from bottom to top and jump periodically every 6 rows due to the change to the next pass. The solution concentration progressively decreases from top to bottom as vapor is absorbed into it.
Variation of vapor absorption rate across the absorber is shown in Figure (7). At the absorber inlet absorption rate is very small as mentioned before and then increases as the solution temperature drops and finally decreases uniformly as the difference between the solution and cooling water temperatures decreases. Figure (8) shows the variation of heat duty across the absorber. At the inlet heat duty is high even though absorption rate is small because of sensible cooling of the solution and then drops toward the bottom with periodic jump every new pass.
CONCLUSION
A mathematical model and a computer Code for development and simulation of a small-size absorption refrigeration machines using LiBr-H2O as working fluid were developed in this study. Operating conditions were selected as input to this model and code and the corresponding absorber geometry to meet these conditions were given as output. The resulted absorber performance was then simulated and presented graphically.
Nomenclature
| = | constants | = | Biot number | ||
| = | specific heat capacity at constant pressure (kJ/kg °C) | ||||
| = | diameter (m) | = | mass diffusivity of solution (m2/s) | ||
| = | Graetz number | = | specific enthalpy (kJ/kg) | ||
| = | heat of absorption (kJ/kg) | = | thermal conductivity (kW/m2 °C) | ||
| = | length (m) | = | Lewis number | ||
| = | mass flow rate (kg/s) | = | number | ||
| = | number of tubes | = | Nusselt number | ||
| = | pressure (kPa) | = | Prandtl number | ||
| = | heat flow per unit length (kW/m) | = | Renolds number | ||
| = | Sherwood number | = | temperature (°C) | ||
| = | mass fraction of water in solution (kg/kg) | ||||
| = | average mass fraction | = | coordinate along wall plate (m) | ||
| = | coordinate perpendicular to the wall plate (m) | ||||
Greek
| | = | dimensionless mass fraction |
| = | average dimensionless mass fraction | |
| = | solution film thickness | |
| = | dimensionless temperature | |
| = | average dimensionless temperature | |
| = | dimensionless heat of absorption | |
| = | lithium bromide concentration (kg/kg) | |
| = | dynamic viscosity (kg/m.s) | |
| = | density (kg/m3) | |
| = | derivative of | |
| = | thermal diffusivity (m2/s) |
Subscripts
| = | sequence number | ||||
| = | absorbed | = | absorber | ||
| = | average | = | cooling water | ||
| = | equilibrium | = | interface or inside | ||
| = | sequence index | = | number | ||
| = | entrance or outside | = | refrigerant | ||
| = | solution | = | vapor | ||
| = | wall |
Superscripts
| = | absorber | = | pass | = | row |
REFERENCES
- Andberg, J.W. and G.C. Vliet, 1987. A simplified model for absorption of vapors into liquid films flowing over cooled horizontal tubes. ASHRAE Trans., 93: 2454-2466.
Direct Link - Beutler, A., I. Greiter, A. Wagner, L. Hoffmann, S. Schreier and G. Alefeld, 1996. Surfactants and fluid properties. Int. J. Refrigeration, 19: 342-346.
Direct Link - Garimella, S., 2000. Microchannel components for absorption space-conditioning systems. ASHRAE Trans., 106: 453-464.
Direct Link - Hoffmann, L., 1996. Experimental investigations of heat transfer in a horizontal tube falling film absorber with aqueous solutions of LiBr with and without surfactants. Int. J. Refrigeration, 19: 331-341.
Direct Link - Jeong, S. and S. Garimella, 2002. Falling-film and droplet mode heat and mass transfer in a horizontal tube LiBr/water absorber. Int. J. Heat Mass Transfer, 45: 1445-1458.
CrossRefDirect Link - Khalid, A.J. and H.A. Lafta, 2001. Simulation of a simple absorption refrigeration system. Energy Convers. Manage., 42: 1575-1605.
CrossRefDirect Link - Yoon, J.I. and E. Kim, 2002. Heat transfer enhancement with a surfactant on horizontal bundle tubes of an absorber. Int. J. Heat Mass Transfer, 45: 735-741.
CrossRefDirect Link








