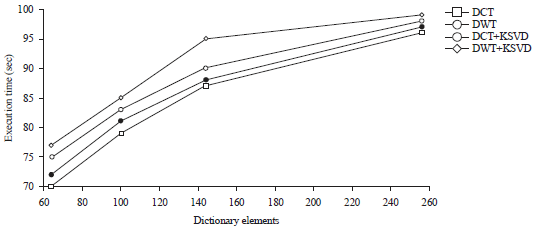
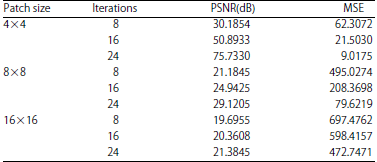
Research Article
Dictionary Properties for Sparse Representation: Implementation and Analysis
Department of Electronics and Communication, Charotar University of Science and Technology, Changa, Gujarat, India
LiveDNA: 91.22100
Hiren Mewada
Department of Electronics and Communication, Charotar University of Science and Technology, Changa, Gujarat, India
LiveDNA: 91.15403