Case Study
A Novel Metric for Comparing the Intelligence of Two Swarm Multiagent Systems
Petru Maior University, Tg. Mures, Romania
Corina Rotar
1 Decembrie 1918 University, Alba Iulia, Romania
Recently, many swarm systems have been used for different problems solving1-3. They are inspired by the collective biological intelligence of relatively simple living creatures, like ants, insects and bugs etc. As examples of such particular approaches, the different type of ants algorithms4 and bees algorithms5,6 was mention. Neural networks sometimes are combined with swarm systems in order to improve their efficiency. In this study7 a particle swarm optimization approach combined with neural computation is presented. The proposal is applied for the recognition of hyper-spectral altered rock.
Many times in the scientific literature a swarm system is considered intelligent when the cooperation even between very simple agents could result in the emergence of intelligence at the level of the swarm, without giving a quantitative evaluation of the intelligence. Such a simple motivation is just an intuitive prove of the existence of the intelligence. It is very important to elaborate metrics that are able to make a quantitative evaluation of the intelligence, thus, allowing also the comparison of swarm system’s intelligence.
In this study, it was concluded that an important aspect that it should be taken into consideration regarding the intelligence measuring of a swarm system, consists of the variability of intelligence (some situations/conditions imply higher intelligence and other situations imply lower intelligence). There were considered that, in the case of some swarm systems, if the variability is not taken into account, it could result in erroneous estimation of the intelligence. Different experimental evaluations for the intelligence level of a system that does not have a deterministic behavior could lead to different conclusions.
In this study, an accurate mathematically grounded metric for comparison of two swarm systems intelligence is proposed. Moreover, swarm systems that use some kind of neural computation could be compared also. There were considered swarm systems composed of simple agents that cooperate based on some simple rules. For demonstrating the effectiveness of the metric, an illustrative case study of two swarm ant system, able to solve the Traveling Salesman Problem (TSP-problem) that is an NP-hard problem was realized.
Bio-inspired intelligence and swarm intelligence: Studies on biological intelligence include: Human intelligence8, animal intelligence9 and plant intelligence10. In biological systems composed of very simple living creature like ants, the intelligence could be considered at the level of the swarm. An ant as an individual does not have intelligence, but cooperating with other ants could solve highly complex problems. Based on this consideration, a biological ant colony could be considered intelligent at the swarm level.
Turing11 considered a computing system intelligent if a human assessor could not decide the nature of the system (being human or otherwise) based on the machine’s answers to some specific questions. The present study outlines the difference between the biological intelligence and artificial intelligence and therefore, they should not be compared directly, being of different types. The biological intelligence is the result of billions of years of evolution on earth. Even the computing systems evolve very fast it would take a long time until they will attain a similar complexity and intelligence with the biological systems.
Important research directions consist in development of algorithms1,2 that attempt to represent the simplified models of different biological swarms. Ants algorithms4 and bees algorithms5 are examples of such particular approaches.
It is important to differentiate the intelligent systems (mostly, agent-based systems) and computational intelligence. The computational intelligence includes some fields of artificial intelligence, like neural networks12,13, fuzzy systems and ant colony optimization14.
If a computing system uses a computational intelligence algorithm, it does not necessarily mean that the system could be considered intelligent. For example, a very simple mobile robotic agent was considered (an embodied robot that operates in a physical environment, perceiving the environment via sensors and executing actions via effectors, which has an agent like properties) that uses a neural network to make predictions. Based just only on the consideration that it uses a neural network, the system could not be considered an intelligent one.
However, intelligent systems could use computational intelligence algorithms. This study focus on intelligent systems, computing systems that are able to solve difficult problems like NP-hard problems. For instance, an intelligent mobile robotic agent could be able to solve highly difficult problems and among others uses a neural network for image recognition. The neural networks belong to the class of methods called computational intelligence.
Artificial swarm systems are based on the simplified model of biological swarms like the ant’s colony. Some artificial swarm systems are able to solve even difficult problems. An intelligent swarm system could have different advantages versus a system that operates as individual that fulfill the same functionalities. Advantages may consist in lower development cost, increased robustness, increased efficiency etc. The proposed metric presented in this study called MetrInt is able to make an accurate comparison of two swarm systems intelligence.
In the following paragraphs, it is proposed a mathematically grounded accurate metric for comparison of two swarm systems’ intelligence. There are considered swarm systems composed of very simple interacting agents that are able to solve difficult problems, at the level of swarm. In each swarm system the agents interact with each other based on some simple rules, which define an elementary low-level but efficient (the agents make simultaneously a distributed search), flexible (the swarm is susceptible of modification or adaptation) and robust (if few agents fail, this does not mean the failure at the swarm level) cooperation.
The two swarm multiagent systems are denoted with SWA and SWB. The SWA is composed of the agents SWA = {SWA1, SWA2,..., SWAn}. The |SWA|, |SWA| = n denotes the cardinality (number of agents) of SWA. The SWB is composed of the agents SWB = {SWB1, SWB2,..., SWBm}. The |SWB|, |SWB| = m denotes the cardinality of SWB.
Algorithm “Swarm system’s intelligence comparison” presents the proposed metric for the intelligence comparison. The SIntA = {SIA1, SIA2,..., SIAr} denotes the measured intelligence indicators obtained during the intelligence evaluation in different simulated scenarios (different problems solving for the evaluation of the problem’s solving intelligence) of the SWA system. The |SIntA| (where, |SIntA| = r) denotes the intelligence indicators sample size. The SIntB = {SIB1, SIB2,..., SIBk} denotes the measured intelligence indicators obtained during the intelligence evaluation in different simulated scenarios of the SWB system. The |SIntB| (where, |SIntB| = k) denotes the intelligence indicators sample size.
A measured intelligence indicator denoted in the following generally as Indr (1) is a weighted sum of more indicators value (denoted with param1, param2,..., paramp), which measure components of intelligence, each of them having a specific weight (weights denoted with weigth1, weigth2,..., weigthr) in the final intelligence indicator value determination, which present the swarm intelligence:
| (1) |
 |
The intelligence comparison is based on a specific mathematical calculus using the indicator’s values obtained as results of some simulations in the case of both swarm systems SWA and SWB. The indicators are retained in SIntA = {SIA1, SIA2,..., SIAr} corresponding to SWA and SIntB = {SIB1, SIB2,..., SIBk} corresponding to SWB. For both swarm systems, the “Extraction” algorithm calculate the central intelligence indicator denoted as CentrIndA and CentrIndB, the standard deviation of central indicators denoted as Standard DeviationA and Standard DeviationB and the samples sizes denoted as |AIntInd| and |BIntInd|. The means of SIntA and SIntB are considered for the calculation of central indicator.
Applying the swarm system’s intelligence comparison algorithm, two swarm systems’ intelligence can be compared. Null hypothesis denoted as H0 represents the statement that the CentrIndA of SWA is equal from the statistical point of view with the CentrIndB of SWB.
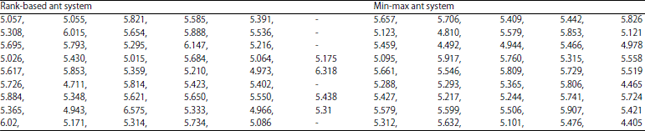
| Table 1: | Simulation results of the two swarm systems |
 | |
| Table 2: | Results of the extraction algorithm |
 | |
Alternative hypothesis denoted as H1 represents the hypothesis that the CentrIndA of SWA is different from the statistical point of view from CentrIndB of SWA. The testing of H0 and H1 is realized with the significance level denoted by α. Alpha (α) is a parameter of the algorithm and represents the probability of rejecting the null hypothesis when it is true (to make a type I error). The value α is set to 0.05.
For the presented swarm system’s intelligence comparison algorithm, the H0 testing is made with the two-sample t-test15 in the case of equality between the standard deviations of SWA and SWB.
If the H0 is verified then it can be concluded that the two swarm system’s intelligence is equal from the statistical point of view. The numerical difference is given by the variability within samples. Performing the measurements in different experimental conditions could conduct to slightly different result.
If H1 is accepted and CentrIndA<CentrIndB then it can be concluded that SWA is less intelligent than the SWB. If H1 is accepted and CentrIndA>CentrIndB then can be concluded that SWB is less intelligent than the SWA.
For proving the effectiveness of the proposed metric the following scenario was set: In the experiments for illustrative purposes, there were considered two swarm systems that operate as a SWA = Rank-based ant system16 and a SWB = Min-max ant system16 and they were applied for a very well known NP-hard problem, the Traveling Salesman Problem (TSP)14,17.
In the case of the rank-based ant system16, the obtained solutions are ranked according to their length. The amount of deposited pheromone is weighted for each solution. However, solutions with shorter paths deposit more pheromone than the solutions with longer paths.
For the min-max ant system16, there are retained both the maximum and minimum pheromone amounts denoted as (max, min). Only the global best and iteration best tour deposited pheromone. All of the edges in the graph are initialized to max and reinitialized to max when stagnation is detected.
The experimental scenario takes into consideration maps with nr = 35 randomly placed cities. The parameters of both algorithms are: Number of tests = 1000, alpha = 1 (power of the pheromone), beta = 1 (power of the distance per edge weight) and evaporation = 0.1 (the evaporation factor).
Table 1 presents the simulation results. In the simulations, it was considered that for both swarm systems, the intelligence indicator is the obtained best to date travel value at the end of the simulation.
Table 2 presents the calculated mean, Standard Deviation (SD) and sample size calculated for SWA and SWB. The statistical equality between the standard deviations of SWA and SWB was verified by using the F-test, obtaining as results: F = 1.079 and the p = 0.8019, p>0.05, suggesting that the equality of standard deviations (the difference between the standard deviations is not statistically significant). Based on the equality of standard deviations of SWA and SWB, according to the algorithm comparison swarm system’s intelligence, it can be concluded that it should furtherly be applied the two-tails unpaired two-sample t-test with α = 0.05.
Applying the unpaired two-sample t-test it was obtained t = 0.9567 and the p = 0.3412. Based on this result p>α, it can be concluded that the difference in intelligence between the two swam systems SWA and SWB are not statistically different for the solving of TSP problem when the map includes 35 cities placed.
There are many definitions of computing system’s intelligence. Based on many years of experience, there were considered that is impossible to give a general/universal unanimously accepted definition. Many definitions presented in the scientific literature are based on some considerations like autonomous learning, self-adaptation and evolution. Moreover, there is required to elaborate metrics that allows an accurate measuring of computing system’s intelligence.
Artificial swarm systems are composed of simple agents, being able solve many problems, including NP-hard problems, like the traveling salesman problem. For a swarm system’s intelligence, it could be given a general definition, mostly based on benefits in cooperation between the agent’s members of the swarm during the problems solving process. Many studies proved that, even for simple efficiently, flexibly and robustly cooperating swarm systems, the intelligence emerge at the swarm level.
It is not enough to give a general definition to a swarm system’s intelligence based just on some intuitive considerations. It was considered that it should be developed accurate metrics that allows an estimation of swarm system’s intelligence and comparisons of the intelligence of more than one swarm systems. Swarm systems could be by different type, specialized on different problems solving. Considering these aspects, adapted metrics should be developed, based on particularities of the systems.
In this study, it was considered that the intelligence is measured at the level of the whole swarm not at individual/agent level. Our metric is appropriate for the swarm systems, where the intelligence indicator for a problem solving by the swarm system is expressed by a single value. This value can be calculated as a weighted sum of some other values if these measure different aspects of the swarm system’s intelligence. The proposed metric takes into account the variability of the intelligence of the compared swarm systems. A swarm system could have different intelligent reactions in different situations. In a specific situation, the swarm system reaction could be more or less intelligent. For instance, we mention the situation when the reaction is more intelligent in some cases and less intelligent for other cases.
This study18 presents a similar metric called MetrIntComp for comparison of two cooperative multiagent systems. The effectiveness of the proposed metric MetrIntComp is proven for a case study. The disadvantages of the MetrIntComp versus the metric MetrInt, proposed in this study include the more limited accuracy and the necessity to use a higher sample size. The main advantage of the MetrIntComp consists in its robustness, as it does not require that the intelligence indicators sample data to be normally distributed. There is possible the effective comparison of the two metrics, both of them measuring the intelligence in a similar way.
This study19 proposes the idea of a general test called universal anytime intelligence test. The researcher of the study consider that such a test should be appropriate to measure the intelligence level (no matter how low or how high it would be) of any biological or artificial system. It is based on the on C-tests and compression-enhanced Turing tests developed in the late 1990s. The authors of the research discuss different tests by highlighting their limitations. They introduce some new ideas that they consider necessary for the development of a “Universal intelligence test”. The main advantage of the metric MetrInt consists in the intelligence comparison based on practical evaluations and based on this; an accurate comparison of two swarm systems should be possible. Without such an approach, considering just a pure theoretical model, it is difficult to make an accurate comparison.
In many studies there are presented some evaluations or analyzes of the system’s intelligence. There are very few effective metrics designed for making a comparison of two or more multiagent systems. In this study20 the collective intelligence of particle swarm system is assessed according to a proposed maturity model. The proposed model is based on the maturity model of command and control operational space and the model of collaborating software. The main aimed of the study was to obtain a more thorough explanation of how the intelligent behaviour of the particle swarm emerges. In this study20 it is presented an approach that is not appropriate for the accurate comparison of two swarm multiagent systems intelligence. The metric MetrInt proposed by us in this study is able to make an accurate comparison of two multiagent systems and allows a classification, also. If two swarm systems have the same intelligence, they can be included in the same class of intelligence.
In this study, it was proposed that a novel accurate metric for comparing two swarm system’s intelligence considering the variability (more or less intelligence that is expressed in different situations). For the validation of our proposed metric, it was considered two swarm ant colony systems, rank-based ant system and min-max ant system, that are specialized in solving the traveling salesman problem-an NP-hard problem. The result of the intelligence comparison based on the proposed metric proves that the small difference regarding the intelligence is the result of an accident (repeating the experiments could result in slightly different results) and therefore, there is no statistically significant difference in the intelligence between the two swarm systems for the considered scenario.
Based on a comprehensive study of the scientific literature, taking into account the lack of such accurate metrics that is also able to compare two swarm systems, it could be stated that the proposed metric is innovative and it will represent the basis for intelligence evaluation in many future researches.