Research Article
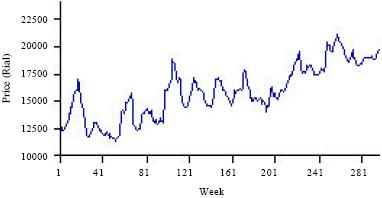
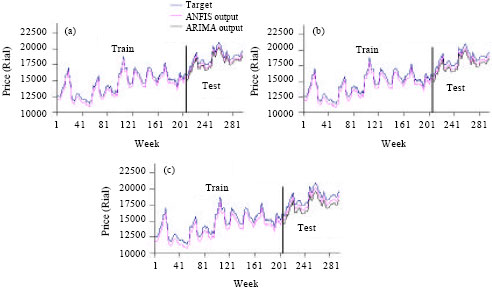
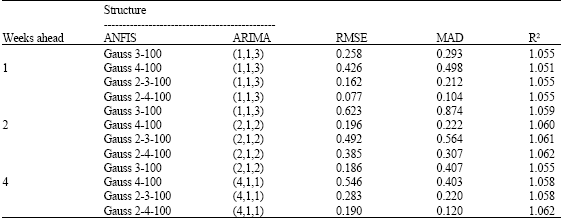
Application of ANFIS to Agricultural Economic Variables Forecasting Case Study: Poultry Retail Price
Department of Agricultural Economics, University of Zabol, Zabol, Iran
M. Salarpour
Department of Agricultural Economics, University of Zabol, Zabol, Iran
M. Sabouhi
Department of Agricultural Economics, University of Zabol, Zabol, Iran
S. Shirzady
Department of Agricultural Economics, University of Zabol, Zabol, Iran












Hamed Reply
Good job and congratulations.