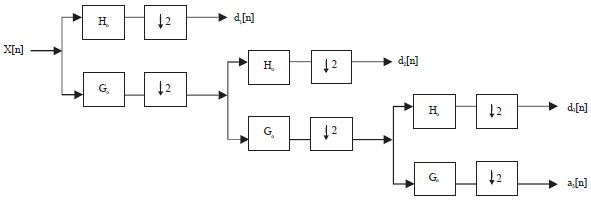
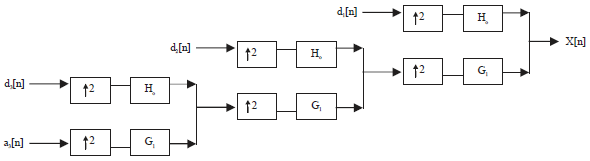
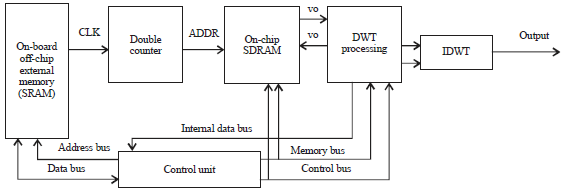
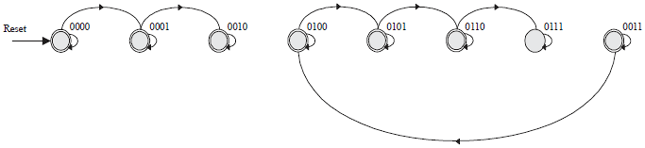
Research Article
Implementation of Wavelet-based Architecture for Optimization Image Filtering
Department of Computing and Engineering Sciences, Babcock University, Ilishan-Remo, Ogun State, Nigeria
LiveDNA: 234.31325
Ajaegbu Chigozirim
Department of Computing and Engineering Sciences, Babcock University, Ilishan-Remo, Ogun State, Nigeria
LiveDNA: 234.24480
Oladejo Daniel Oluwaninyo
Department of Computing and Engineering Sciences, Babcock University, Ilishan-Remo, Ogun State, Nigeria