Research Article
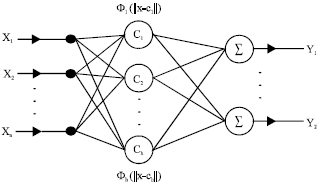
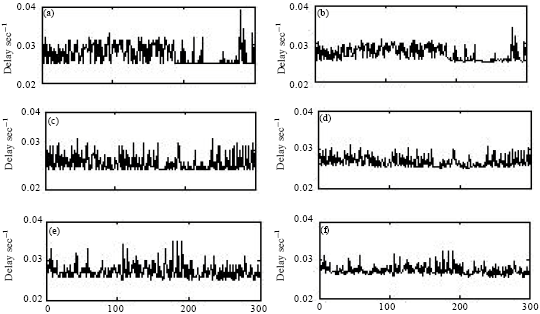
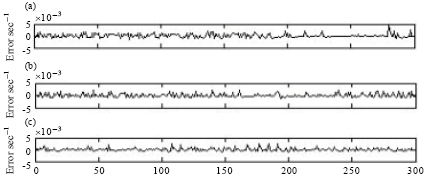
Research of Delay Prediction Based on RBF Neural Network
School of Control and Computer Engineering, North China Electric Power University, Beijing, 102206, China
Pengfei Jin
School of Control and Computer Engineering, North China Electric Power University, Beijing, 102206, China
Kai Li
State Grid Xinjiang Information and Telecommunication Company, Urumqi, 830000, China