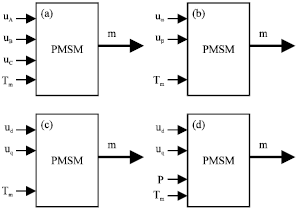
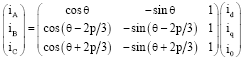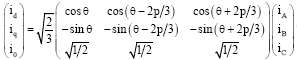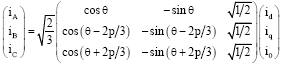Research Article
Modeling and Simulation of Permanent Magnet Synchronous Motor Vector Control
School of Computer Science and Technology, Henan Institute of Engineering, China
Jianli Kang
School of Architectural and Artistic Design, Henan Polytechnic University, China