Research Article
The 7-DOF Automatic Fiber Placement Manipulator’s Self-motion Manifold
College of Electrical and Information Engineering, Xuchang University, 461000, China
In the manufacturing process of the aircraft S-shaped inlet, advanced automatic fiber placement technology is used. The fiber is placed automatically on the mandrel by the end-effector according to the pre-planned trajectory (Liu, 2011; Zhu et al., 2011). The robotic manipulator has at least 6 Degrees of Freedom (DOF) to place the fiber on mandrel but the 6-DOF robotic manipulator can not track mandrel position in arbitrary orientation. Therefore, some scholars improved the robotic manipulator’s tracking goal capability by increasing DOF, in other words to improve the robotic manipulator’s dexterousness, the DOF by additional is called redundant DOF; this robotic manipulator with additional DOF is called redundant robotic manipulator (Han et al., 2009; Yang et al., 2011). Redundant robotic manipulator has more flexibility and better obstacle and singularity avoidance capability than robotic manipulator has less than 6-DOF (Lu, 2007; Zhang et al., 2004). So, studying 7-DOF redundant robotic manipulator is more meaningful. The inverse kinematics is the basis of planning and motion control for robotic manipulator which is the same as redundant robotic manipulator. The first need is to solve the inverse kinematics problem if trajectory planning and motion control are to be achieved. Redundant robotic manipulator’s self-motion manifold contains all the inverse kinematics (Moll and Kavraki, 2004; Muller, 2004; Zhao et al., 2007, 2009; Xinfeng and Dongbiao, 2012; Zhang et al., 2011; Kazem et al., 2010), shows the mapping relationship between the end-effector and joints and reflects the self-motion ability essentially.
Inverse position should be obtained in order to get self-motion manifold, the inverse position is difficult to solve for redundant robotic manipulator whose DOF is more than 6. Inverse kinematics based on self-motion manifold are all the inverse kinematics, therefore, analyzed the redundant automatic fiber placement robotic manipulator’s self-motion manifolds which has some reference to analyzing inverse kinematics of other type redundant robotic manipulators.
The self-motion manifold is used to obtain the all inverse kinematics solutions of the redundant robotic manipulators. The position space manifold and orientation space manifold are defined at first, then the self-motion manifold could be obtain by pairing the position space manifold and orientation space manifold, at last verified by example.
7-DOF AUTOMATED FIBER PLACEMENT REDUNDANT ROBOTIC MANIPULATOR’S TOPOLOGY
The automatic fiber placement robotic manipulator’s structure is shown in Fig. 1a. From its structure, there is a 6-DOF fiber placement robotic manipulator and a rotational mandrel. According to the principle of equivalence movement: mandrel coordinate system is fixed with the base coordinate system, a virtual revolute joint linked the base and the mandrel together, Rotational mandrel is equivalent to the robotic manipulator’s rotation around the base. So the fiber placement robotic manipulator with 6-DOF and the mandrel with 1-DOF becomes a 7-DOF redundant robotic manipulator. The shoulder has a revolute joint, the elbow has three prismatic joint, wrist has three revolute joint. The three revolute joint axes of the wrist intersect at one point, the automatic fiber placement robotic manipulator’s topology after equivalent motion as shown in Fig. 1b.
 | |
| Fig. 1(a-b): | Automated fibre placement robotic manipulator’s structure and topology. 1: Tailstock, 2: Mandrel, 3: Chuck, 4: Link, 3, 5: Link, 2, 6: Link, 1, 7: Placement head, 8: Link, 6, 9: Link, 5, 10: Link, 4, 11: Mandrel part and 12: Manipulator part |
| Table 1: | Parameters of the automated fiber placement robotic manipulator |
 | |
Establishing D-H coordinate system and its structural parameters as shown in Table 1.
REDUNDANT ROBOTIC MANIPULATOR SELF-MOTION MANIFOLD
Position space manifold of redundant robotic manipulator: The end-effector position can be obtained easily by the 7th joint coordinate system original position. The definition of moving coordinate system does not affect analyzing the robotic manipulator’s kinematics, so the end-effector coordinate system can be assumed coinciding with the 7th joint coordinate system. The automated fibre placement robotic manipulator’s three prismatic joints intersect at one point and determined the end-effector’s spatial position. Then the end-effector position is determined by the ![]() , the
, the ![]() is the vector between intersection of the 5, 6 and 7th joint axis and origin of the base coordinate system, all such
is the vector between intersection of the 5, 6 and 7th joint axis and origin of the base coordinate system, all such ![]() constitutes the redundant robotic manipulator’s position work space, so the three prismatic joints is also called position joints.
constitutes the redundant robotic manipulator’s position work space, so the three prismatic joints is also called position joints.
According to the equivalent motion of the automatic fiber placement robotic manipulator, waist, shoulder and elbow’s configuration space can be defined as:
| (1) |
The redundant robotic manipulator’s position space Up can be expressed as:
| (2) |
Here, fp is the map from CWSC to Up; θp = [θ1, d2, d3, d4]T.
Either take ![]() ∈ UP position space manifold is defined which the vector
∈ UP position space manifold is defined which the vector ![]() is corresponding to:
is corresponding to:
| (3) |
Cp is directly called position space manifold.
The redundant fiber placement robotic manipulator orientation joint manifold: Three revolute joints axis on wrist intersect at point O4, end-effector orientation adjustment can be carried out only by the 5, 6 and 7th joints’ rotation and position of point O4 does not change when end-effector orientation adjusts. Three revolute joints on wrist are also called orientation joints. Then the redundant robotic manipulator is decoupled in position and orientation.
The wrist joints configuration space is defined as:
| (4) |
Assuming ![]() and
and ![]() for the given θpkεCp. When the robotic manipulator is in some singularity, kinematics redundant will occur when adjusting wrist joints orientation. Assuming:
for the given θpkεCp. When the robotic manipulator is in some singularity, kinematics redundant will occur when adjusting wrist joints orientation. Assuming:
orientation joints manifold which the vector pair (θpk, z7O4, y7O4) is corresponding to is defined:
| (5) |
Similarly, Co is directly called orientation joint manifold.
The redundant fiber placement robotic manipulator self-motion manifold: The redundant fiber placement robotic manipulator’s end-effector position workspace can be expressed by the position space manifold; end-effector orientation can be expressed by two coordinate axes vector z7 and y7 of the 7th joint. Any one point on the position workspace manifold corresponds to a orientation space, the orientation space can be described as all the vector pairings (z7, y7) which matched by axis z7 and axis y7 of the 7th joint coordinate system on the point, end-effector orientation space can be described as all the vector pairings of ![]() .
.
The joint space of the ith joint can be expressed as Ci and then the joint configuration space C can be expressed as seven separated product space of Ci:
| (6) |
The role of robotic joint is equivalent to the role of functions in mathematics which implements mapping and inverse mapping between the joint configuration space and the end-effector position and orientation workspace. Assuming θ = [θ1, θ2, L, θ7]T, so the redundant robotic end-effector position and orientation workspace can be described as:
| (7) |
Where, f can be obtained by direct kinematics of redundant robotic manipulator.
Either takes vector uεU, so the self-motion manifold which corresponded to by vector u can be described as a pairing that composed by a configuration subspace CSO and a set of mappings FSO:
| (8) |
f is easy to obtain by θ for the redundant robotic manipulator, therefore, the main task which solves redundant robotic manipulator self-motion manifold is to solve CSO and CSO is called the redundant robotic manipulator self- motion manifold.
THE AUTOMATIC FIBER PLACEMENT REDUNDANT ROBOTIC MANIPULATOR SELF-MOTION MANIFOLD
Three revolute joint axes of the automatic fibre placement robotic manipulator wrist intersect at one point and determined the robotic manipulator end-effector’s orientation in the work space; three prismatic joint axes intersect at one point and determined the robotic manipulator end-effector’s position in the workspace. The end-effector’s orientation can be achieved only by three wrist joints and the end-effector position can not be moved, so the robotic manipulator’s self-motion manifold can be divided position space manifold and orientation space manifold. The position space manifold and orientation space manifold can be solved, respectively; the robotic manipulator self-motion manifold can be obtained by pairing them.
The redundant automatic fiber placement robotic manipulator position space manifold: Assuming position and orientation transformation matrix is ![]() which coordinate system T fixed the end-effector relative to coordinate system fixed the mandrel S, there have:
which coordinate system T fixed the end-effector relative to coordinate system fixed the mandrel S, there have:
 | (9) |
The position joint can be calculated according to Eq. 9:
 | (10) |
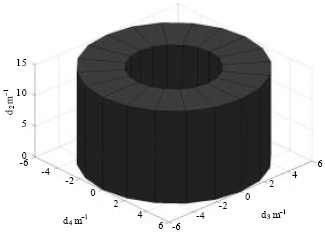 | |
| Fig. 2: | Automatic fiber placement redundant robotic manipulator position space manifold |
According to the equivalent movement principle, assuming the automatic fiber placement redundant robotic manipulator end-effector tracked a spatial circular in its work space, the automatic fiber placement redundant robotic manipulator’s position space manifold is shown in Fig. 2.
But in actual fiber placing process, the robotic manipulator end-effector actual route is a spatial curve in Fig. 2, in addition to the part to be paved size limits; the position space manifold is a portion of Fig. 2.
The automatic fiber placement redundant robotic manipulator orientation joint manifold: The three revolute joints of the robotic manipulator intersect at one point, the geometric structure as shown in Fig. 3. The desired coordinate of the end-effector is (xee, yee, zee) under the coordinate system X0Y0Z0, the distance from the point to the end-effector is l , ψ is an angle between two planes, one is a vertical plane through the first joint, the other is that contain the end-effector and its projection on the X0Y0 plane.
The following equations were established according to the automatic fibre placement redundant robotic manipulator orientation joint geometric structure:
| (11) |
| (12) |
| (13) |
The inverse kinematics can be solved according to Eq. 11-13 and for given (xee, yee, zee) and ψ:
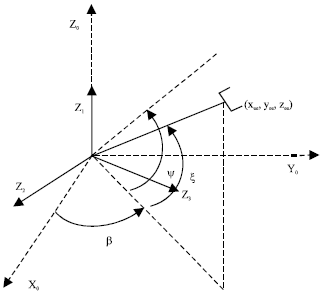 | |
| Fig. 3: | Automatic fibre placement redundant robotic manipulator orientation joint geometric structure |
 |
The automatic fiber placement redundant robotic manipulator self-motion manifold: Redundant robotic manipulator self-motion manifold is the sub manifold of the configuration space manifold. The redundant automatic fiber placement robotic manipulator self-motion manifold is paired by the position space manifold and the orientation joint manifold. The redundant automatic fiber placement robotic manipulator orientation joint manifold is a plane curve and the position space manifold is a hollow cylinder at θ5 = 0, therefore the redundant automatic fiber placement robotic manipulator self-motion manifold is a plane curve in the hollow cylinder.
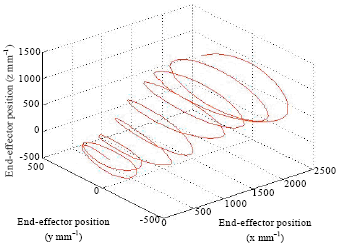 | |
| Fig. 4: | Desired trajectory of end-effector |
The redundant automatic fiber placement robotic manipulator orientation joint manifold is a spatial curve at θ5 ≠ 0, the redundant automatic fiber placement robotic manipulator self-motion manifold is a spatial curve in the hollow cylinder, consequently, the 7-DOF redundant fiber placement robotic manipulator can complete the fiber placement task in any orientation.
VERIFICATION THE REDUNDANT AUTOMATIC FIBER PLACEMENT ROBOTIC MANIPULATOR SELF-MOTION MANIFOLD
In order to verify the correctness of the self-motion manifold solved, the redundant automatic fiber placement robotic manipulator placing some S-shaped inlet mandrel which is taken as an example, using the inverse kinematics solved by self-motion manifold to verify. Figure 4 is desired trajectory of the redundant automatic fiber placement robotic manipulator end-effector on the mandrel, Fig. 5 shows the simulation trajectory of the redundant automatic fiber placement robotic manipulator end-effector which using the inverse kinematics solved and desired trajectory.
According to the desired fiber placement trajectory, the simulation fiber placement trajectory of the end-effector can be obtained by self-motion manifold and shown in Fig. 5. Compared to Fig. 4, simulation fiber placement trajectory obtained is good agreement with desired fiber placement trajectory, the redundant automatic fiber placement robotic manipulator self-motion manifold solved in this paper is correct. Ma (2005) proposed the actual joint configuration and the desired joint configuration is consistent in the self-motion manifold; Yao et al. (2009) and Zhao et al. (2007, 2009) planned the robotic motion by using self-motion manifold.
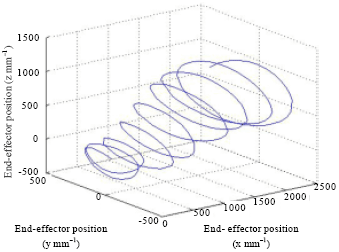 | |
| Fig. 5: | Simulation trajectory of end-effector |
The 7-DOF redundant automatic fiber placement robotic manipulator is the redundant robotic manipulator which its position and orientation are decoupled and its self-motion manifolds can be seen as which the position space manifold and the orientation joint manifold paired. When solving the redundant robotic manipulator self-motion manifold whose position joint and orientation joint decoupled, the redundant robotic manipulator self-motion manifold can be decomposed the position workspace manifold and orientation workspace manifolds, then analyzed and solved, respectively. Finally, the redundant robotic manipulator self-motion manifold can be obtained by pairing the position workspace manifold and the orientation workspace manifold.
This study is financially supported by National Natural Science Foundation of China (51275479), to express my gratitude.