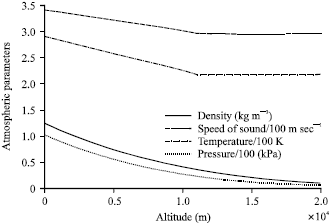
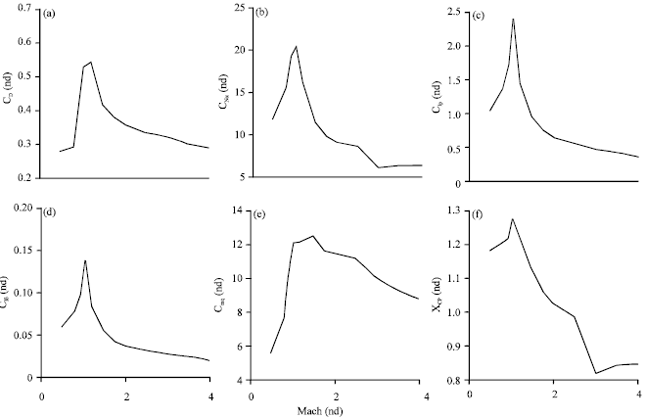
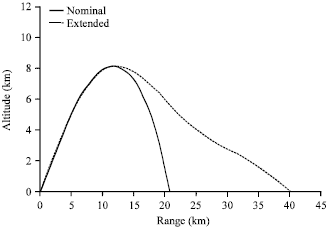
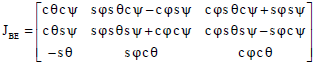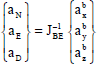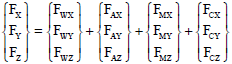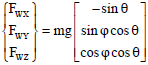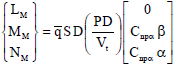Research Article
Extended Range of Fin Stabilized Projectile Using Movable Canards
National Key Laboratory, Nanjing University of Science and Technology, 200 XiaoLing Wie, XuanWu, Nanjing, Jiangsu, 210094, China
YI Wen-Jun
National Key Laboratory, Nanjing University of Science and Technology, 200 XiaoLing Wie, XuanWu, Nanjing, Jiangsu, 210094, China