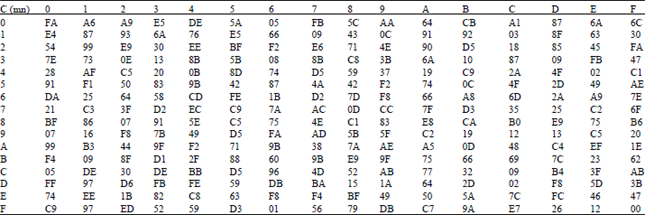
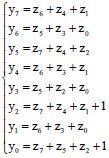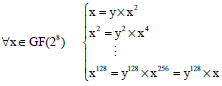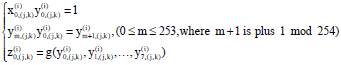Research Article
Generation and Optimization of Rijndael S-box Equation System
School of Computer Science and Technology, Anhui University, Hefei, 230039, China
Hong Zhong
School of Computer Science and Technology, Anhui University, Hefei, 230039, China
Jiankai Wang
School of Natural Sciences, Anhui Agricultural University, Hefei, 230036, China
Runhua Shi
School of Computer Science and Technology, Anhui University, Hefei, 230039, China