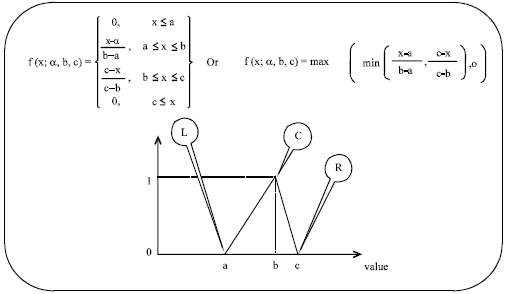
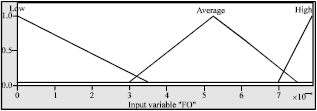
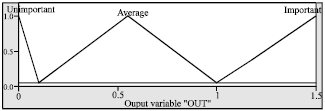
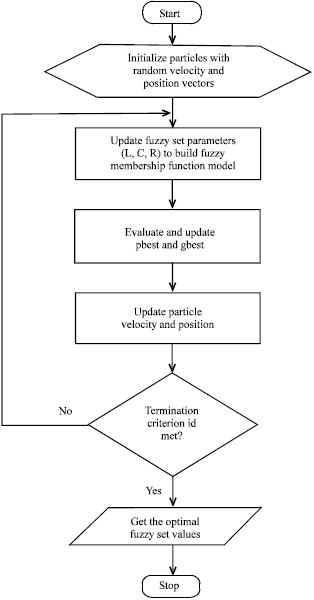
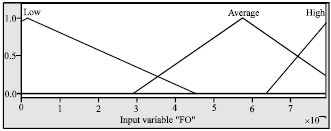
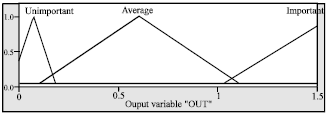
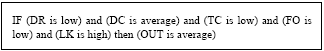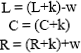Research Article
Term Extraction Using Hybrid Fuzzy Particle Swarm Optimization
Faculty of Computing, Universiti Teknologi Malaysia, Skudai, Johor, 81310, Malaysia
Naomie Salim
Faculty of Computing, Universiti Teknologi Malaysia, Skudai, Johor, 81310, Malaysia