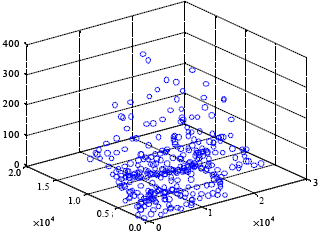
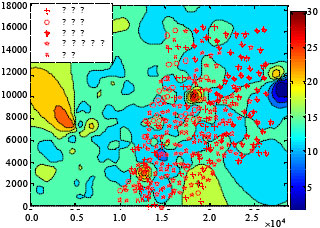
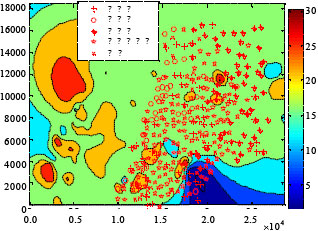
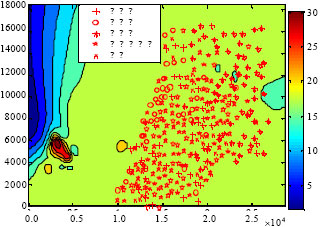
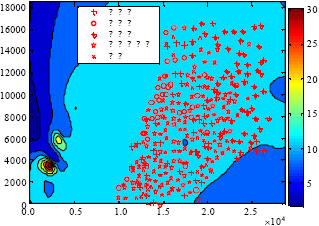
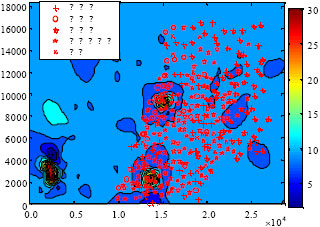
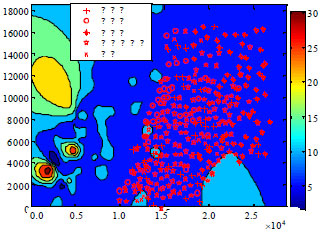
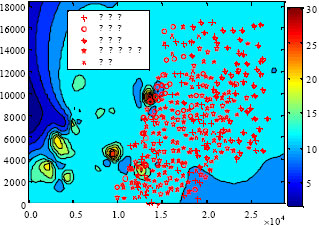
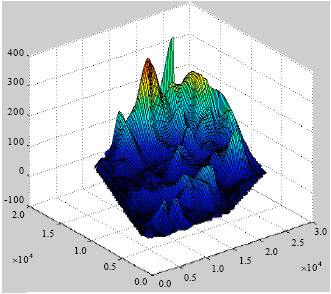
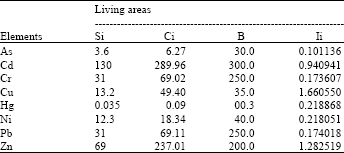
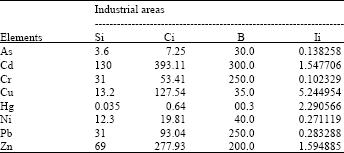
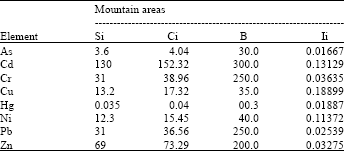
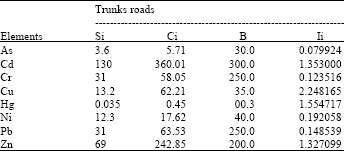
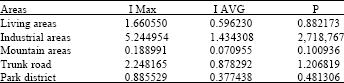
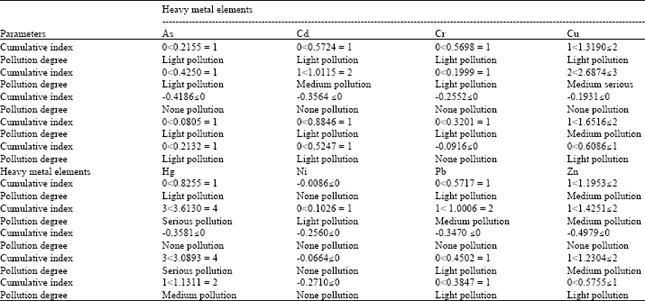
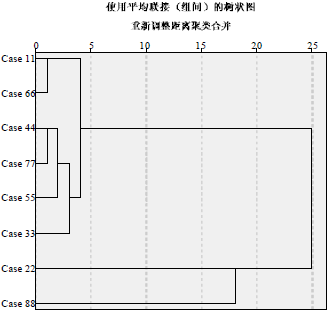
Research Article
Analysis of Heavy Metal Pollution in Urban Topsoil
College of Science, Xi`an University of Technology, Xi`an, 710048, China
Xin Ji
College of Science, Xi`an University of Technology, Xi`an, 710048, China
Wei Wei
School of Computer Science and Engineering, Xi`an University of Technology, Xi`an, 710048, China
Wen Wen
College of Science, Xi`an University of Technology, Xi`an, 710048, China