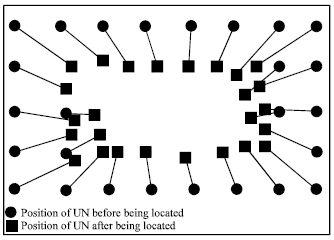
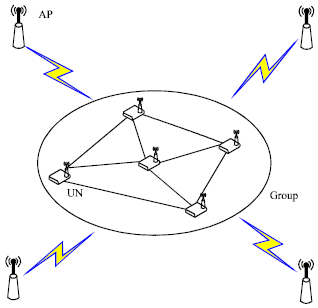
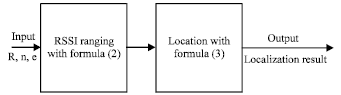
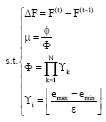
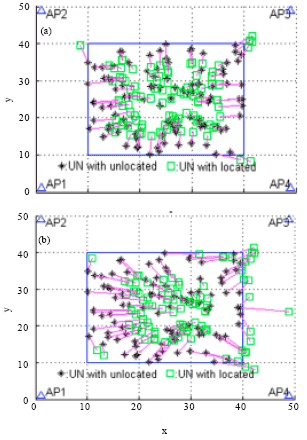
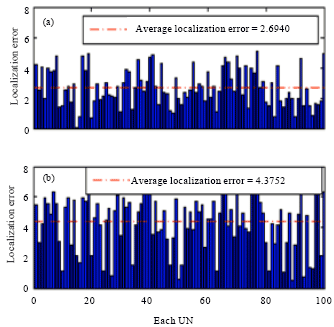
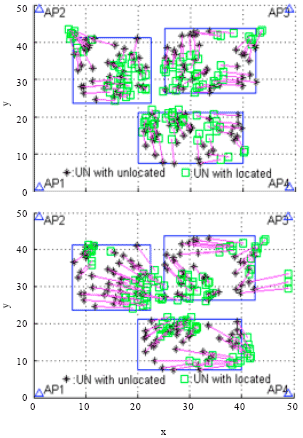
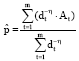Research Article
An Adaptive RSSI Compensation Strategy Based on Simulated Annealing for Indoor Cooperative Localization
College of Automation, Chongqing University, Chongqing 400030, China
Wei-Ren Shi
College of Automation, Chongqing University, Chongqing 400030, China
Wei Zhou
College of Automation, Chongqing University, Chongqing 400030, China
Hong-Bing Li
College of Automation, Chongqing University, Chongqing 400030, China
Xiao-Gang Wang
College of Automation, Chongqing University, Chongqing 400030, China