ABSTRACT
Estimate request service demand is vital for resource management and capacity planning in large web servicing system. Most existing works assume the service demand is load-independent. This study showed that it is not the case for modern processors with Dynamic Frequency Scaling (DFS) and Simultaneous Multi-Threading (SMT) capabilities. Through experiments in a Xeon processor under Linux, this study showed that the CPU demand can be modeled as a polynomial function of CPU utilization with degree 2 or 3. This study proposed a quadratic programming based optimization method to infer the polynomial coefficients from readily available CPU utilization and response time data. Comparing with widely used regression method, proposed optimization method can reduce the error by more than half in most cases. Proposed method is also more accurate than the existing load-dependent estimation method, particularly in workload of requests with different sizes.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/itj.2013.632.639
URL: https://scialert.net/abstract/?doi=itj.2013.632.639
INTRODUCTION
Large web service systems are becoming complex and hard to manage. In such systems, one key to manage the resources is a deep understanding of the service demand of various web requests (Pacifici et al., 2008). When CPU is the resource of interest, the service demand of a request, or the CPU demand, is the total CPU processing time of a request. It does not include the queueing time and the time taken in other resources due to remote invocation. Accurate CPU demand estimation can help to answer capacity related questions, such as “What if the ratio of ordering requests to browsing requests increases by 30%?”
Estimating the service demand is an active research field. Most existing works assume the service demand of a request is load-independent. This assumption, however, no longer holds as the CPU design get more complex. In a modern CPU, such as Nehalem based Xeon processor of Intel, two techniques are employed to provide the CPU with dynamic performance. As a result, the CPU demand can scale up or down with the load. Dynamic Frequency Scaling (DFS) technique enables the CPU to lower the core frequency when idle and to increase the frequency when busy. In other words, the CPU is faster in high load and slower in light load (Zhang and Li, 2012). Simultaneous Multi-Threading (SMT) also called hyper-threading by Intel, enables the processor to run multiple streams of instructions simultaneously in a single core to exploit Instruction Level Parallelism (ILP). Operating Systems (OS) treat each CPU thread as a logic CPU but the processing power of a logic CPU is not equal to that of a real one. In fact, at higher load, the logic CPUs become slower due to the increasing contention of processor internal resources among multiple threads (Magro et al., 2002).
To better model the load-dependent behavior of CPU demand in the modern CPU induced by DFS and SMT, we propose to represent the CPU demand as a function of CPU utilization, instead of a constant. Through experimental evaluation, the function is chosen to be a polynomial function of degree 2 or 3. The coefficients of the polynomial function can be inferred using Quadratic Programming (QP) techniques from common performance data in production or testing environment, such as CPU utilization, request throughput and response time.
SERVICE DEMAND ESTIMATION RESEARCH
Performance models, especially queueing network models, are important tools for performance analysis. The parameterization of the performance model is an important research topic. In the queueing network model, service demand is one of the most important parameters. However, it is very hard to measure directly (Anandkumar et al., 2008). Most works opt to use indirect estimation method.
Indirect estimation method utilizes some inherit relationship between service demand and other measurable performance metrics and uses statistical method to infer unknown service demand. The most commonly used performance metrics are resource utilization and request response time. According to the utilization law, resource utilization is linearly related to service demand, so various linear regression techniques can be used (Zhang et al., 2008; Pacifici et al., 2008; Casale et al., 2008; Kalbasi et al., 2011). Response time is related to service demand in a nonlinear manner which is specified by the performance model itself. Various linear or nonlinear optimization techniques can be used to estimate service demand from response time with or without other performance metrics such as resource utilization and throughput (Liu et al., 2006; Kraft et al., 2009).
Most existing works of indirect estimation assume the service demand is constant. However, load-dependent queue has long been used in queueing theory to model load-dependent behavior widely present in computer systems (Sauer, 1983; Rak et al., 2010). Unlike our assumption that the demand is a function of CPU utilization, load-dependent queue assumes the service demand is a function of the number jobs currently in the queue. However, to the best of our knowledge, few methods are available to estimate such load-dependent function. Most works derive the function from prior knowledge specific to the target field. For example, the disk seek time was found to increase inversely with the number of queued requests (Padhye and Rahatekar, 1995). Other works start with a complex queueing network then abstract part of the system as a load-dependent queue using flow equivalent server method (Menasce et al., 2004). However, the load-dependent function cannot be obtained if the original queueing network is unknown. Kumar et al. (2009) investigated the general problem of estimating load-dependent demand. They modeled the service demand as a polynomial function of total workload throughput. The total throughput was further subject to optional logarithmic and exponential transformation which we found unnecessary when modeling DFS and SMT related load-dependent behavior. To estimate the parameters of the demand function, they used an optimization method similar to Liu et al. (2006). Our previous work investigated the load-dependent behavior due to DFS (Zhang and Li, 2012). This study proposed to incorporate average CPU frequency metric into the classical regression method to estimate the service demand of CPU at highest frequency. The demand at highest frequency can be used to predict system resource capacity but cannot predict the response time at specific load.
LOAD-DEPENDENT BEHAVIOR IN MODERN CPU
Take the Xeon X5560 processor as an example, the processor has 4 cores and offers both DFS and SMT capabilities. X5560 has two processor threads for each core, 8 cores in total. X5560 can switch between 10 frequency levels ranging from 1.6 to 2.8 GHz. DFS and SMT are well supported by the OS. We take Linux kernel 2.6.18 and Xeon X5560 as the reference OS and processor, respectively.
Linux supports SMT by treating each CPU thread as a logic CPU. Threads of the same core share resources such as processor buffers and internal processing units. Multiple threads can run in parallel when accessing different shared resources. However, when they are accessing the same shared resources in the same time, some of them must wait. As a result, the processing speed of logic CPUs depend on the CPU load; the higher the load, the slower the logic CPUs become. The speed scaling factor depends on the degree of instruction level parallelism of the workload (Magro et al., 2002). The lower the ILP, the more the speed of logic CPUs varies.
Linux supports DFS via various frequency change policies. Linux defaults to the on demand policy which is a dynamic policy. When the CPU is busy, it switches CPU to the maximum frequency; when the CPU becomes idle, it gradually lowers the CPU frequency until the minimum frequency is reached. The speed scaling factor under on demand policy depends on the request size, i.e., service demand of requests in the workload (Zhang and Li, 2012). The smaller the request size, the more the speed of CPUs varies.
This study experimented with different single-class workload and calculated the service demand using the utilization law. The detail of workload and experiment environment is introduced in the experiment section. In order to separate the impact of SMT and DFS on request processing, we disabled each of these two functions through sysfs interfaces. In particular, this study disabled SMT by disabling the second logic CPU of each core; we disabled DFS by fixing the frequency at the maximum frequency state. To ensure the number logic CPUs is consistent in various setting, we disabled all 4 logic CPUs of two cores when SMT was enabled.
Figure 1 shows how the CPU demand of a particular request scales with the CPU utilization under different DFS and SMT setting. If both DFS and SMT are disabled, the CPU demand remains stationary when the load increases. This is exactly the traditional expectation of CPU demand. If only DFS is enabled, the CPU demand decreases in a nonlinear manner with the increasing load and nearly halves in high load comparing to that in light load.
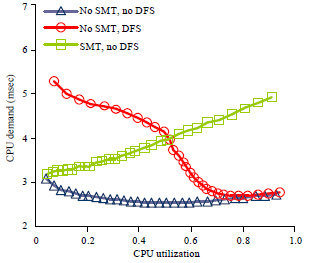 | |
| Fig. 1: | CPU demand scaling in different SMT and DFS setting |
The scaling factor corresponds to the inverse of CPU frequency ratio (2.8/1.6 GHz). If only SMT is enabled, the CPU demand gradually increases with the load in a linear fashion and almost doubles in high load comparing to that in light load. Note that the above two demand curves are extreme examples of how SMT and DFS influence CPU demand, the actual degree of scaling of an arbitrary request may be modest. If both DFS and SMT are enabled, the demand scaling has both increasing and decreasing factors and the final shape of the demand curve depends on which effect is dominant.
Figure 2 shows various typical CPU demand curves when both DFS and SMT are enabled. Since these curves differ significantly in CPU demand values, to fit them in a single figure, we normalized the CPU demand values of each curve by dividing the values with the one measured at the lightest load. In the figure, there are both gradually increasing and decreasing patterns which correspond to DFS dominant and SMT dominant cases, respectively. When the contradicting influence of DFS and SMT reach a balance (Balance I), the CPU demand resembles a concave quadratic curve. In another balance situation (Balance II), the CPU demand resembles a sinusoid curve which can be fit using with a cubic function. As suggested by the cases of Balance I and II, the relative strength of SMT and DFS vary with the load.
Figure 2 suggests that the typical CPU demand curves can be fit with polynomial functions of degree 2 or 3. We calculated the coefficient of determination (R2) of the polynomials to quantify the degree of fitness.
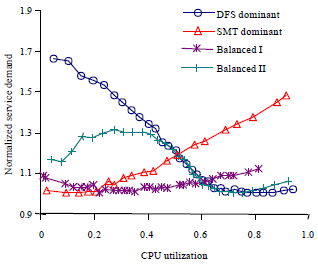 | |
| Fig. 2: | Typical demand curves when both SMT and DFS are on |
The closer R2 approaches to 1, the better the function can fit the curve. We found that the fitness is quite good (R2>0.9) for most curves. The only exception is that the polynomial function of degree 2 cannot accurate fit the Balance II curve (R2 = 0.67) which is similar to a sine curve. We conclude that it is possible to use polynomial functions to closely approximate the scaling behaviors of CPU demand.
LOAD-DEPENDENT ESTIMATION
The target system in this study is a typical multi-tier system. Such system is often modeled as an open queueing networks which includes a tandem of queues where each queue corresponds to the major resource in a tier (Liu et al., 2006; Kumar et al., 2009). This study only consider the CPUs, so each queue corresponds to a physical processor. The end user requests can be classified into multiple classes according to URL patterns. Different class of requests can have different CPU demand at various queue. The problem of service demand estimation is how to estimate CPU demand of each queue using readily available performance data such as CPU utilization and end-to-end request response time.
Since CPU demand is load-dependent for modern CPU, we represent the CPU demand as a function of CPU utilization. The previous section shows that polynomial functions of degree 2 or 3 can fit the CPU demand closely:
| (1) |
Here, assume that the CPU demand function only depends on the CPU utilization. In other words, given the CPU utilization, the function is independent of other workload attributes, such as the mix proportion of multi-class workload. In practice, as we will show in the next section, the assumption is not strictly true, because there are interference effects between classes. Nevertheless, this assumption greatly simplifies the estimation problem and is a close approximation to the reality in most cases. Note that we choose the CPU utilization as the load indicator, not other metrics such as the overall throughput ![]() as in previous work (Kumar et al., 2009). If CPU demand is a function of the overall throughput, then the coefficients of the polynomial can change greatly across different mixes which makes the function too volatile to be useful for prediction.
as in previous work (Kumar et al., 2009). If CPU demand is a function of the overall throughput, then the coefficients of the polynomial can change greatly across different mixes which makes the function too volatile to be useful for prediction.
To obtain CPU demand, one must infer the unknown coefficients of the polynomial. These coefficients are bound by some constraints. Firstly, the CPU demand is always positive, so, sj0,i = sji (0)>0. Secondly, the experiments summarized in Fig. 2 show the shape of quadratic or cubic functions. The quadratic function is a concave function, so, aj2,i≥0; the cubic function is convex at low load and concave at high load, so, aj3,i≥0. One can estimate these coefficients from the utilization law:
| (2) |
where, aj0,i>0, aj2,i>0 if n = 2 and aj3,i>0 if n = 3. Here, εi is an error tem which must be minimized.
The response time can also be used for demand estimation. However, we found that modern multi-core multi-thread processor cannot be modeled simply as multi-server queues due to the complex load balancing mechanism among multiple CPUs (Bligh et al., 2004). Therefore, we propose to use multi-server queues as inequality constraints of the CPU demand. In particular, the response time is between the predictions of two extreme case models, M/M/c queue and parallel M/M/1 queues (Gunther, 2005):
| (3) |
Here, we denote the residence time of class j requests in processor i when utilization is ρi as Rji (ci, ρi) , where ci is the number of servers in the multiple server queue. Rji (ci, ρi) is calculated using Erlang’s C function.
In practice, the above hard inequality constraint can be violated in some time intervals. For example, even in a system where the arrival process is basically Poisson, there are some time intervals where the arrival process may be bursty thus deviate from Poisson. To avoid rendering the estimation problem infeasible due to the abnormal data, soft constraints are preferred over hard constraints. We relax the inequality constraints by introducing two sets of slack variables δ and ξ which quantify the violation of the constraints:
| (4) |
where, δj≥0, ξj≥0.
One has to ensure the degree of violation is minimal, so the estimation problem in optimization form is as follows:
| (5) |
One can obtain multiple sets of ρ and R, each of which corresponds to a single measurement time interval. To fit multiple sets of data, we use the sum of these objective functions as the overall objective function and the union of all constraints as the overall constraints.
The optimization problem can be solved using standard algorithms for QP (Dostal, 2009). In this study, we use the QP algorithm implemented in Octave program. This algorithm is based on an iterative active-set method. To speed up the convergence of QP, we initialize the QP problem using the regression technique with constant CPU demand assumption (Zhang et al., 2008).
To predict the server utilization, one can solve Eq. 2 for unknown ρ which amounts to find the roots of the polynomial function. When multiple solutions of ρ exist, we simply choose the smallest feasible solution (ρ∈[0,1]); if no real solution exists, we first discard the image part of all solutions then choose the smallest feasible solution.
EXPERIMENTS
The experimental environment was based on a simple client-server architecture which consists of a server with X5560 processor and a client PC interconnected by a 100 Mb sec-1 switched Ethernet, that is, I = 1. The server used tomcat6 to host micro-benchmarking servlets. The workload is CPU-bound, thus IO time is negligible. The client used JMeter to emulate client browsers which visit the server through HTTP. The CPU utilization of the server was measured by the Sysstat tool every 2 min. The server was quiescent when no request arrives, that is, no service was running except Tomcat6 and Sysstat. The response time and throughput were measured by JMeter. In our environment the client PC and network was lightly loaded, the sum of time taken at the client and network was roughly 1 msec. We reported the response time excluding client and network time.
We used 3 micro-benchmarking servlets: int_mem, dbl_mem, int_dbl. These servlets are quite similar to the one introduced (Magro et al., 2002). The int_mem servlet does controllable iterations of interleaved integer arithmetic operations and memory access; the dbl_mem servlet does controllable iterations of interleaved floating arithmetic operations and memory access; the int_dbl servlet does controllable iterations of interleaved floating and integer arithmetic operations. The dbl_mem servlet is actually identical to int_mem, except that the type of data variables changes to “double”. Table 1 shows the workload characteristics of requests for these servlets reported by OProfile tool. In the workload of these requests, memory access can be satisfied in the large CPU cache of Xeon, so, the main ILP is the overlapping of integer and float instructions. Thus, int_dbl has the highest ILP while int_mem has the lowest ILP. The CPU demand and inter-arrival times of each class of requests were generated from exponential distribution; the arrival rates were slowly increased to vary the CPU utilization from 0% to nearly 90%.
We study the accuracy of the proposed CPU demand estimation method in a multi-class workload. We compare our proposed load-dependent method (LDU) with:
| • | The regression method: the state of art load-independent estimation method (LI) |
| • | The method introduced Kumar et al. (2009): the only load-dependent method known so far which models the demand as a function of total request throughput (LDX) |
Since response time cannot be used as equality constraints in modern CPUs, we modify the original LDX method to use soft inequality constraints as in our LDU method.
The multi-class workload is summarized in Table 2. Two groups of test scenarios were used, one for requests with different ILP, the other for requests with different sizes (service demand). In each scenario, two classes of requests were applied to the system (J = 2) and the mix proportion of two classes varied. The first class of requests in turn accounted for 0.2, 0.4, 0.6 and 0.8 of the total throughput, i.e., 4 different mixes for each scenario (named 0.2, 0.4, 0.6 and 0.8).
| Table 1: | Workload characteristics of different requests |
 | |
| IPC: Instructions per cycle, PF: Float point instructions | |
| Table 2: | Multi-class workload |
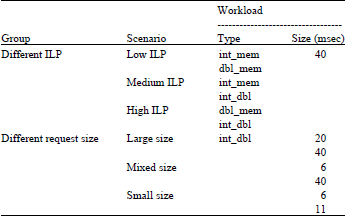 | |
The total number of data entries (each for a time interval) in each scenario was around 160 and the data was split into two subsets with the same size but different mix proportion. One subset contained the mix 0.2 and 0.4, the other contained the mix 0.6 and 0.8. We derived the load-dependent CPU demand from one of the subset and used the other for test.
This study used quadratic functions to fit the CPU demand. Our implementation of the proposed estimation method usually converged within 500 iterations and took 60-200 sec in a Duo Core machine with 2.0 GHz frequency. We also tried to fit the model using cubic functions; the algorithm usually converged faster than the one using quadratic functions. However, their accuracy was roughly the same, so we omit the result of cubic functions.
Prediction accuracy: To validate the accuracy of the CPU demand estimation method, for each time interval, we calculated the relative error of the CPU utilization prediction (|ρpredict-ρreal|/ρreal).
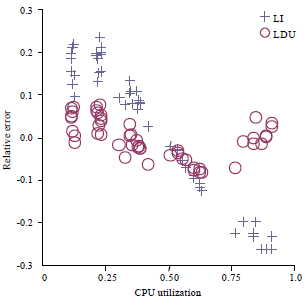
We used the average of the relative errors of all time intervals as the validation metric. The lower the relative error, the higher the estimation accuracy is. The role of training and testing was interchanged and we reported the average of relative errors calculated before and after the interchange. Figure 3 shows the relative errors for all scenarios. We found that our load-dependent method (LDU) is more accurate than the Load-independent (LI) and the previous load-dependent method (LDX).
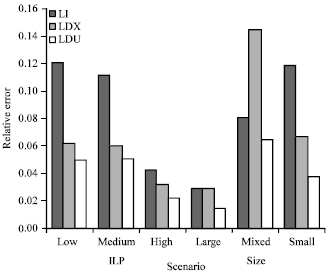 | |
| Fig. 3: | Utilization prediction error |
In all scenarios except Mixed scenario, LDU more than halves the relative error comparing to LI; in Mixed scenario, the relative error of LDU is also significantly smaller than that of LI. In three of the scenarios, the prediction error of LI exceeds 10% which is generally considered a threshold for acceptable accuracy (Menasce et al., 2004). In contrast, the LDU is always below the 10% threshold.
We further investigated the error distribution of LI across load. The error of LI at high and light load is significantly larger than its average error. For example in Low scenario (Fig. 4), the error is close to 5% at average load (ρ ≈ 50%), but as large as 20% at high (ρ ≈ 80%) and light (ρ ≈ 20%) load. In contrast, the error of LDU is always below 10%. Note that Low scenario is a typical SMT dominant case, so the CPU demand curve is mostly an increasing curve. LI overestimates the demand at light load and underestimates the demand at high load. In contrast, LDU slightly overestimates the demand at both light and high load.
LDU is also noticeably more accurate than LDX, especially in the scenarios where the size of requests differs. For example in Mixed scenario, the relative error of LDU is less than half of that of LDX. In particular, at high load, the relative error of LDX is more than 50% while the one of LDU is less than 13%.
We investigated the estimated polynomial coefficients of LDX in Mixed scenario trained from the large mixes (mix 0.2 and 0.4) and the small mixes (mix 0.6 and 0.8). The large mixes have more large requests than the small mixes have. We found that the polynomials trained from the large mixes differ vastly with those trained from the small mixes, especially for coefficients of higher order. For example, a2 trained from these two mixes differs by more than one order of magnitude.
 | |
| Fig. 4: | Utilization prediction error distribution in Low scenario |
It is because that the total throughput of large mixes is much smaller than that of the small mixes at the same CPU utilization. Our LDU method uses a more proper load indicator: the CPU utilization, so the estimated polynomials are more consistent across different training sets. Nevertheless, these polynomials do changes across training sets as shown below.
Interference effects: We investigated the polynomials of LDU estimated from different training sets in the medium (ILP) and Mixed (size) scenarios. We found that these polynomials indeed differ. This implies that requests of multiple classes can influence each other in load-dependent behavior.
Figure 5 shows the CPU demand curves in medium scenario estimated from two training sets: int_dbl mixes and int_mem mixes. The int_dbl mixes contain mostly int_dbl requests and the int_mem mixes contain mostly int_mem requests. The demand derived in these two sets are almost the same. However, the demand of the int_mem requests grows slightly slower in int_dbl mixes than in the int_mem mixes. This is possibly because of the parallel execution of integer instructions in int_mem requests and float instructions in int_dbl requests which increases the ILP of the int_dbl mix. Similarly, the demand of int_dbl requests grows more slower at high load in the int_mem mixes than in the int_dbl mixes. In this scenario, the main demand scaling effect is SMT, so we conclude that there is weak interference between requests of multiple classes due to SMT.
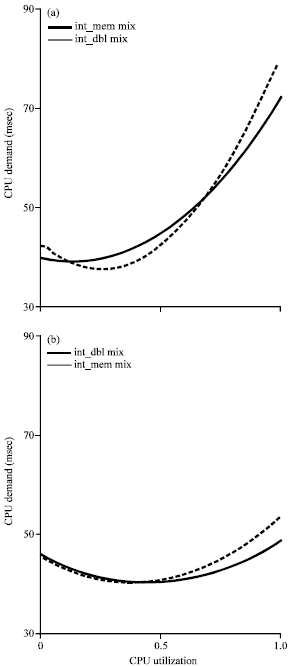 | |
| Fig. 5(a-b): | Estimated CPU demand in medium scenario; (a) Int-mem request and (b) Int-dbl request |
Figure 6 shows the CPU demand curves in mixed scenario estimated from two training sets: the large mixes and the small mixes. The large mixes contain more large requests than the small mixes do. The demand derived in these two sets is similar but differ quite a lot. The demand of small requests decreases more slowly in the large mixes than in the small mixes. This may be the result that intermixed large requests raise the system frequency to high level. Similarly, the demand of large requests also varies more in the small mixes than in the large mixes. In this scenario, the main demand scaling effect is DFS, so we conclude that there is interference effect between requests of multiple classes due to DFS.
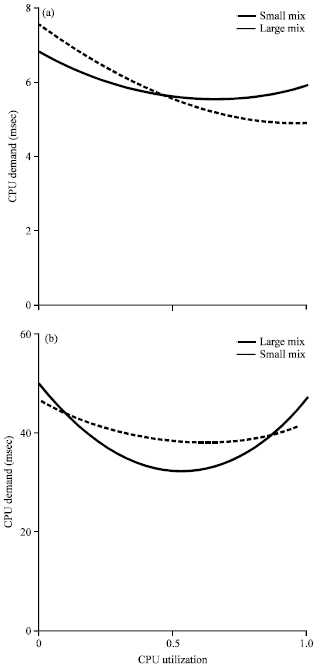 | |
| Fig. 6(a-b): | Estimated CPU demand in mixed scenario; (a) Small request and (b) Large request |
The interference is much stronger than the one due to SMT. This explains why the error reduction of proposed load-dependent method in Mixed scenario is much smaller than in other scenarios.
CONCLUSION
We investigated the phenomenon of load-dependent CPU demand induced by DFS and SMT and found that the load-dependent behavior can be modeled using a polynomial function of degree of 2 or 3. The coefficients of the polynomial can be inferred from performance data using a quadratic optimization method with a set of soft constraints. Extensive experiments using a synthetic workload showed that the method is more accurate than the classic regression method and the existing load-dependent estimation method. One interesting observation is that the load-dependent behavior is also dependent on the mix proportion, especially for the DFS dominant case. So our method should be used with care when predicting the utilization in a significantly different mix than the training mix, especially when the mixed workload contains both large and small requests. It is interesting to explore the load-dependent behavior in other CPU and OS. X5560 is a typical multi-core multi-thread CPU with DFS capability, so, in theory the proposed estimation method can be used in other similar CPUs, such as other Nehalem based CPU or later generations of Xeon CPU. In particular, in recent CPUs with Turbo Boost and virtualization support, the load-dependent behavior can be more complex, so the fitness of polynomial functions should be investigated. In other OS, the DFS policy may differ significantly with the one in Linux, so the demand scaling behavior, such as the form of load-dependent function should also be investigated.
NOMENCLATURE
| J | = | Number of request classes |
| I | = | Number of processors (queues) |
| Pi | = | Number of logic CPUs in processor i |
| ρi | = | CPU utilization of processor i |
| λj | = | Arrival rate for requests of class j |
| Rj | = | End-to-end response time for requests class j |
| sji (ρi) | = | CPU demand of class j requests in processor i when CPU utilization is ρi |
REFERENCES
- Anandkumar, A., C. Bisdikian and D. Agrawal, 2008. Tracking in a spaghetti bowl: Monitoring transactions using footprints. ACM SIGMETRICS Perform. Eval. Rev., 36: 133-144.
CrossRef - Casale, G., P. Cremonesi and R. Turrin, 2008. Robust workload estimation in queueing network performance models. Proceedings of the 16th Euromicro Conference on Parallel, Distributed and Network-based Processing, February 13-15, 2008, Toulouse, France, pp: 183-187.
CrossRef - Kalbasi, A., D. Krishnamurthy and J. Rolia, 2011. MODE: Mix driven on-line resource demand estimation. Proceedings of the 7th International Conference on Network and Services Management, October 24-28, 2011, Paris, France, pp: 1-9.
Direct Link - Liu, Z., L. Wynter, C.H. Xia and F. Zhang, 2006. Parameter inference of queueing models for IT systems using end-to-end measurements. Perform. Eval., 63: 36-60.
CrossRef - Magro, W., P. Petersen and S. Shah, 2002. Hyper-threading technology: Impact on compute-intensive workloads. Intel Technol. J., 6: 58-66.
Direct Link - Pacifici, G., W. Segmuller, M. Spreitzer and A. Tantawi, 2008. CPU demand for web serving: Measurement analysis and dynamic estimation. Perform. Eval., 65: 531-553.
CrossRef - Rak, M., R. Aversa, B. di Martino and A. Sgueglia, 2010. Web services resilience evaluation using LDS load dependent server models. J. Commun., 5: 39-49.
CrossRefDirect Link - Sauer, C.H., 1983. Computational algorithms for state-dependent queueing networks. ACM Trans. Comput. Syst., 1: 67-92.
CrossRef - Zhang, Q., L. Cherkasova, N. Mi and E. Smirni, 2008. A regression-based analytic model for capacity planning of multi-tier applications. Cluster Comput., 11: 197-211.
CrossRef - Zhang, Z. and S.P. Li, 2012. DVFS-aware CPU service time estimation method. J. Zhejiang Univ. Eng. Sci., 46: 725-733.
Direct Link








