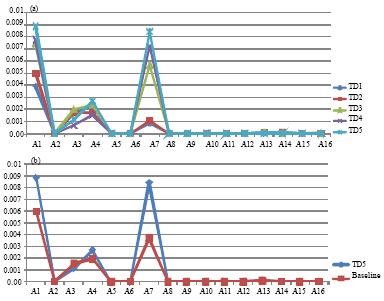
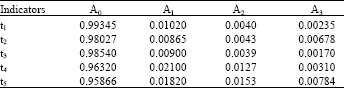
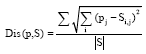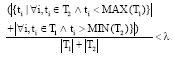Research Article
Anomaly Detection in Transactional Sequential Data
School of Computer Science and Engineering, Guilin University of Electronic Technology, Guilin, 541004, China
Yuming Lin
School of Computer Science and Engineering, Guilin University of Electronic Technology, Guilin, 541004, China
Huibing Zhang
School of Computer Science and Engineering, Guilin University of Electronic Technology, Guilin, 541004, China
Qing Yang
Electronic Engineering and Automation Institute, Guilin University of Electronic Technology, Guilin, 541004, China