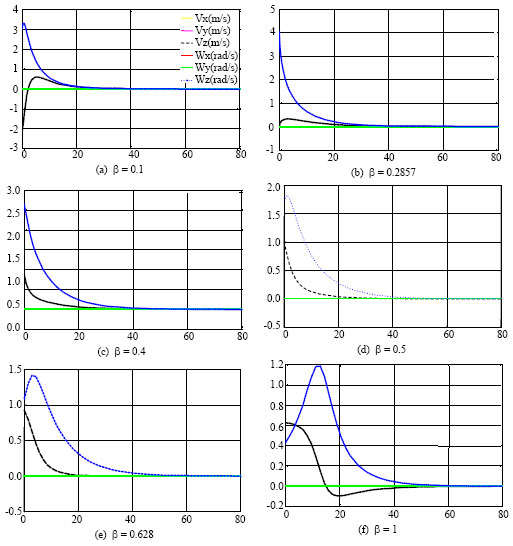
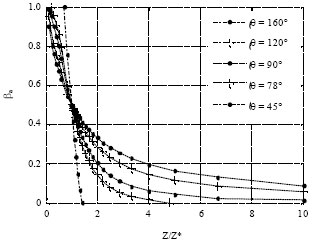
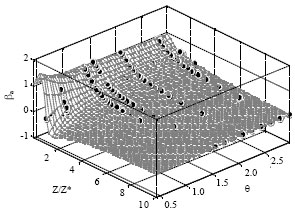
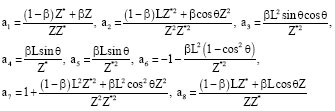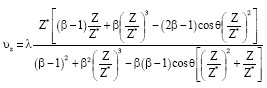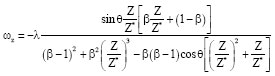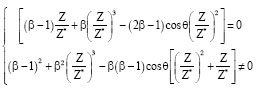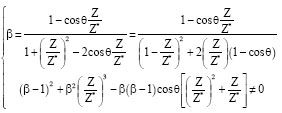Research Article
An Approach to Identify Behavior Parameter in Image-based Visual Servo Control
Faculty of Electronic Information and Electrical Engineering, School of Innovation Experiment, Dalian University of Technology, Dalian 116024, People�s Republic of China
Yue Sun
Faculty of Electronic Information and Electrical Engineering, School of Innovation Experiment, Dalian University of Technology, Dalian 116024, People�s Republic of China
Bo Jin
Faculty of Electronic Information and Electrical Engineering, School of Innovation Experiment, Dalian University of Technology, Dalian 116024, People�s Republic of China
Lin Feng
Faculty of Electronic Information and Electrical Engineering, School of Innovation Experiment, Dalian University of Technology, Dalian 116024, People�s Republic of China