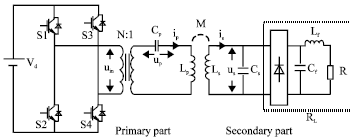
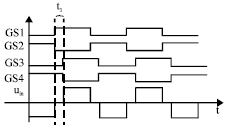
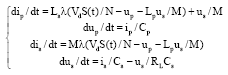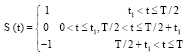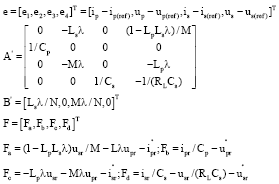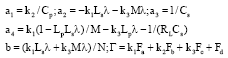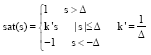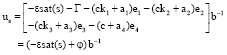Research Article
A Quasi Sliding Mode Output Control for Inductively Coupled Power Transfer System
College of Automation, Chong-Qing University, Chong-Qing, China
Xiao Lv
College of Automation, Chong-Qing University, Chong-Qing, China
Zhihui Wang
College of Automation, Chong-Qing University, Chong-Qing, China
Chunsen Tang
College of Automation, Chong-Qing University, Chong-Qing, China