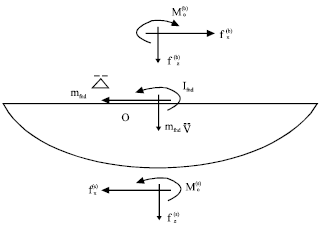
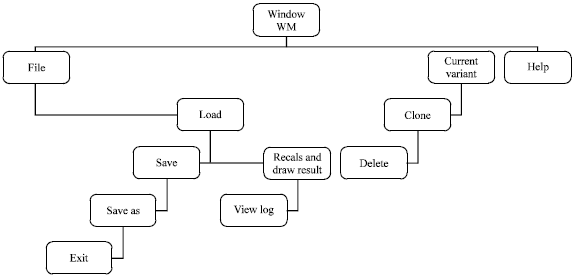
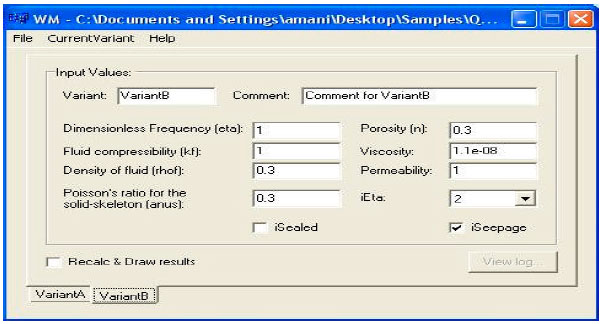
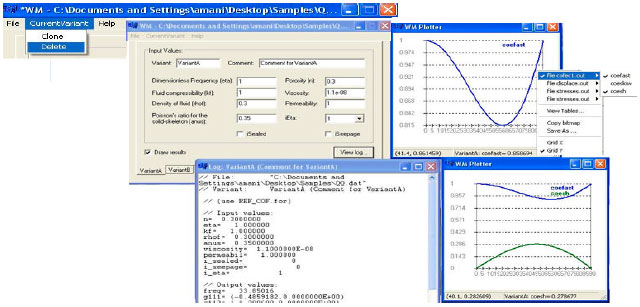
Research Article
Maintenance and Reengineering of Software: Creating a Visual C++ Graphical User Interface to Perform Specific Tasks Related to Soil Structure Interaction in Poroelastic Soil
Department of Computer Engineering, Faculty of Engineering, Philadelphia University, United of States of America
Amani Tahat
Department of Physics and Nuclear Engineering, Technical University of Catalonia-Barcelona Tech, B4-B5 North Campus UPC, 08034 Barcelona, Catalonia, Spain
Jordi Marti
Department of Physics and Nuclear Engineering, Technical University of Catalonia-Barcelona Tech, B4-B5 North Campus UPC, 08034 Barcelona, Catalonia, Spain
Mohammad Tahat
Department of Civil Engineering, New Mexico State University, United States of America