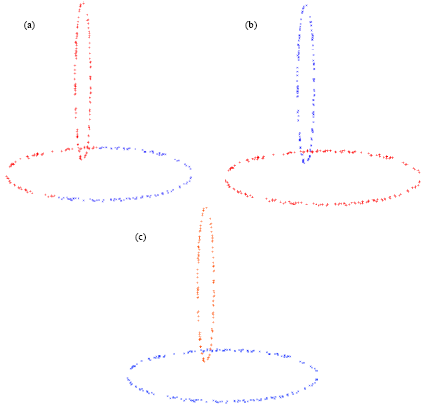
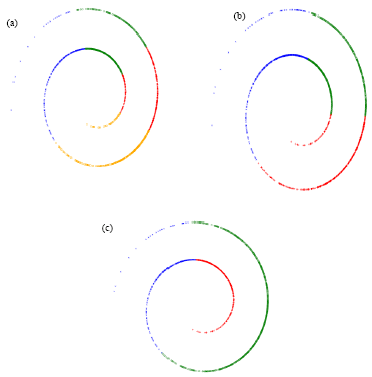
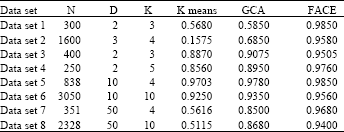
Research Article
A Fast Evolutionary Algorithm for Automatic Evolution of Clusters
Department of Computer Science and Engineering, India
K. Ashiwini
Faculty of Engineering and Technology, Mody Institute of Technology and Science, Lakshmangarh, Rajasthan, India
Sahoo Laxman
School of Computer Engineering, KIIT University, Bhubaneswar, India