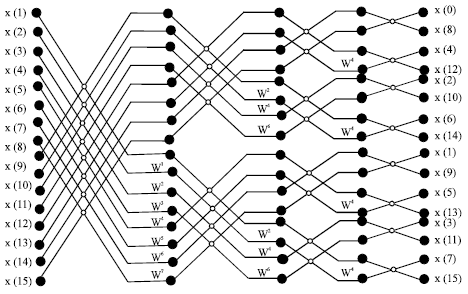
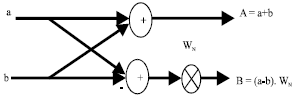
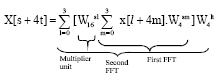
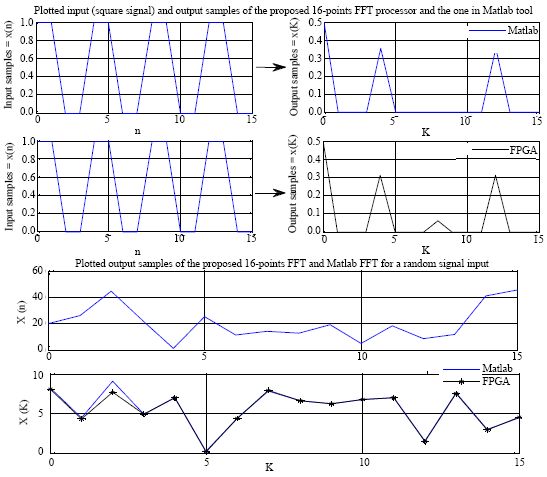
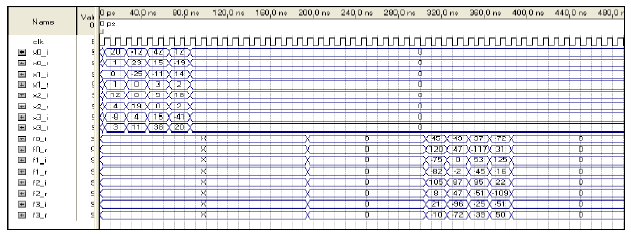
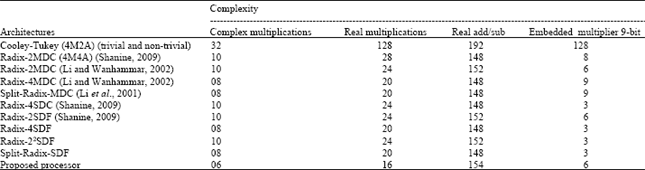
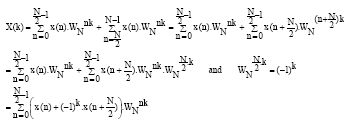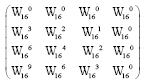Research Article
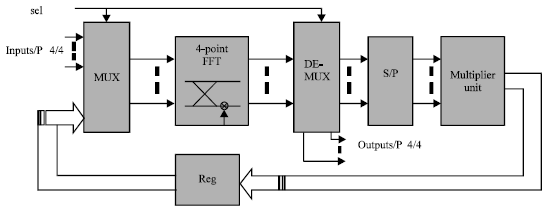
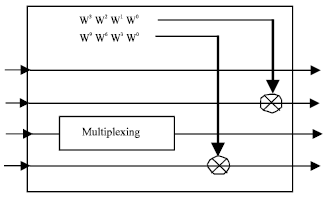
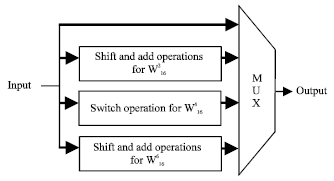
Efficient 16-points FFT/IFFT Architecture for OFDM Based Wireless Broadband Communication
Electronic and Instrumentation Laboratory, Faculty of Science Semlalia, Cadi Ayyad University, Marrakech, Morocco
S. Belkouch
Embedded Systems and Digital Controls Laboratory, Department of Electrical Engineering, ENSAM, Cadi Ayyad University, Marrakech, Morocco
M. M. Hassani
Electronic and Instrumentation Laboratory, Faculty of Science Semlalia, Cadi Ayyad University, Marrakech, Morocco