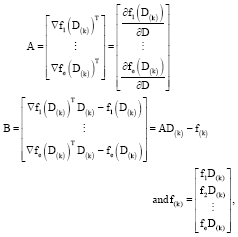
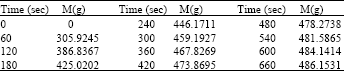
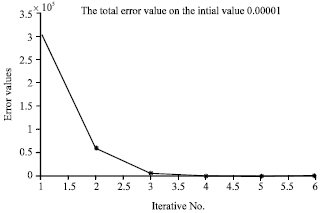
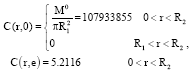Research Article
An Optimal Control Model and the Computer Algorithm for the Diffusion Parameter of the Drug Releasing in the Spherical Device
College of Mathematics, Changsha University of Science and Technology, Hunan, 410004, China
M. Dong
College of Mathematics, Changsha University of Science and Technology, Hunan, 410004, China
X. Xiang
Department of Computer Science, Hunan City University, Hunan, 413000, China
Z. Xiang
College of Mathematics, Changsha University of Science and Technology, Hunan, 410004, China
Y. Pang
College of Mathematics, Changsha University of Science and Technology, Hunan, 410004, China