Review Article
Privacy Preserving Data Publishing: Current Status and New Directions
School of Information and Electronic Engineering, Zhejiang Gongshang University, Hangzhou, 310018, China
The explosive growth of internet has increased the dependence of both organizations and individuals on sharing information universally. This has led to an ever-increasing demand to protect information from unintended use and to guarantee the privacy of involved parties as highlighted by a few incidents. In October, 2006, Netflix, the world’s largest online DVD rental service, announced the $1-million prize for improving their recommendation service and publicly released 100, 480, 507 movie ratings by 480, 189 subscribers for contestants to use. Narayanan and Shmatikov (2006) demonstrated that 96% of Netflix subscribers can be uniquely identified with knowledge of no more than 8 movie ratings and dates. Thus, the second Netflix Prize competition had to be called off at the last minute due to the privacy issues.
In August of 2006, American Online provided an extremely large query log representing 20 million queries issued by 650 K users to help researchers in the information retrieval community. Barbaro and Zeller (2006) demonstrated the ease to determine the real identity of an anonymous AOL searcher, Thelma Arnold, a 62-year-old woman who lives in Lilburn, Georgia, by examining query terms even ignoring the existence of social security numbers, driver license numbers and credit card numbers.
Privacy preserving data publishing, abbreviated as PPDP, emerged to address the privacy issues as illustrated by the preceding incidents.
 | |
| Fig. 1: | Process model of PPDP |
As discussed in Liu (2010) and summarized by the process model in Fig. 1, PPDP addresses such a problem: A trusted data publisher, e.g., Alice in a clinic, collects personal data of individuals, e.g., patients such as Ahmed, in the raw form, anonymizes the collected data and releases the anonymized data to a data recipient or the public, e.g., Bob in a medical research centre. The data publisher, Alice, is responsible for preventing the data recipient, Bob, from breaching the privacy of the individuals, Ahmed, and for retaining usefulness of the anonymized data for data analysis, e.g., for Bob to conduct medical research. The challenge is that the legitimate data recipient, Bob, could be a privacy adversary which makes PPDP even harder than information security.
Since the pioneering work by Samarati and Sweeney (1998), research communities have proposed many approaches to PPDP. While the research field is still rapidly developing, it is a good time to discuss the assumptions and principles of PPDP and systematically evaluate different approaches to PPDP. In particular, the state of the art research works on PPDP are summarized along five dimensions, namely privacy protection principles, anonymization techniques, data utility metrics, algorithms, challenges and future directions.
PRIVACY PRINCIPLES
Generally speaking, privacy is the claim of individuals to control when, how and to what extent information about them is communicated to others. A privacy protection principle enables users to specify the level of privacy protection against a certain type of privacy risk. In PPDP, k-anonymity and l-diversity are well known principles.
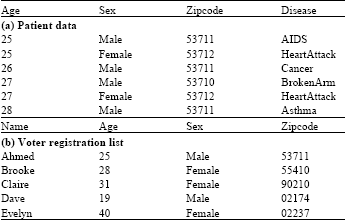
k-Anonymity: Samarati and Sweeney (1998) in their pioneering work discussed an example of PPDP depicted in Fig. 1, where Alice in the clinic submits its patient data, after removing all explicit identifying attributes, e.g., Name, to Bob in the medical research centre. The released data as in Table 1a seems to be anonymous. However, Bob happened to have a voter registration list as in Table 1b that is publically available and joined the two datasets on Age, Sex and Zipcode to find out that Ahmed is the only person who contracted AIDS which violates Ahmed’s privacy and is called linking attack.
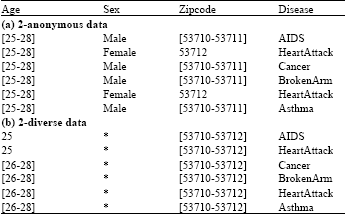
To protect the identities of individuals whose records are in the data to be released, Samarati and Sweeney (1998) proposed the k-anonymity principle. A dataset satisfies k-anonymity if every individual’s record is indistinguishable from at least k-1 other records on quasi-identifier, i.e., attributes that can be used to link with external data, e.g., Age, Sex and Zipcode. For example, data in Table 2a observes 2-anonymity by generalizing attributes Age and Zipcode, where records are partitioned into two indistinguishable groups. The first indistinguishable group consists of records 1, 3, 4 and 6 and the second is made of records 2 and 5.
| Table 1: | Patient data and voter registration list |
 | |
l-Diversity: Machanavajjhala et al. (2006) identified homogeneity attack on the sensitive attribute. For example, attribute Disease is sensitive and the data are 2-anonymous in Table 2a but the values of Disease in the second indistinguishable group (records 2 and 5) are homogeneous, i.e., all are Heart Attack which violates the privacy of the two related persons.
To address the homogeneity attack, Machanavajjhala et al. (2006) proposed the l-diversity principle which requires that there are at least l well-represented values for a sensitive attribute in each indistinguishable group of records. For example, data in Table 2b observes 2-diversity, where records 1 and 2 comprise the first group and others comprise the second group.
More privacy principles: Many privacy principles are intended to thwart specific privacy risks that were not addressed by k-anonymity and l-diversity.
Privacy template was proposed by Wang et al. (2005) which represents the privacy requirement by templates of the form: “A set of identifying attributes”→ “the sensitive information to be protected” associated with a maximum confidence threshold.
(X, Y)-privacy was proposed by Wang and Fung (2006) in considering the privacy attacks based on the linking between two disjoint sets of attributes X and Y. It requires that each value on X is linked to at least k distinct values on Y, namely (X, Y)-anonymity and that the confidence of inferring a value x on X to a value y on Y is less than a given threshold, namely (X, Y)-linkability. k-Anonymity is the special case of (X,Y)-anonymity where X is the quasi-identifier and Y is a key that uniquely identifies records. l-Diversity has some similarity with (X,Y)-linkability in that both bounds the attacker’s inference confidence.
Personalized privacy was proposed by Xiao and Tao (2006b) in addressing the major drawback of k-anonymity and l-diversity, that is, a universal approach that exerts the same amount of protection for all persons, without considering their concrete needs.
| Table 2: | Anonymized patient data |
 | |
t-Closeness was proposed by Li et al. (2007) which requires that the distance between the distribution of a sensitive attribute in an indistinguishable group and the distribution of the attribute in the whole data is no more than a threshold t. Notice that t-closeness has to be used with k-anonymity.
l+-Diversity was proposed by Liu and Wang (2010b) which avoids a universal protection that could incur excessive data distortion by setting a different privacy threshold for each sensitive value according to its sensitivity. Such a notion provides better protection for more sensitive values and incurs less data distortion.
(k,e)-Anonymity was proposed by Zhang et al. (2007) for protecting numerical sensitive attributes, while l-diversity considers only categorical sensitive attribute. This principle requires that each indistinguishable group of records holds at least k different sensitive (numerical) values and the range of sensitive values in the group is no less than a threshold e.
(ε, m)-Anonymity was proposed by Li et al. (2008) to prevent the proximity attack on numerical sensitive attributes. Such privacy attack occurs when an adversary concludes with a high confidence that the sensitive value of a victim individual must fall in a short interval. This principle demands that for every sensitive value x in an indistinguishable group of records, at most 1/m of the records in the same group can have sensitive values similar to x in the ε-neighborhood of x. This means sensitive values should be well distributed, i.e., scattered in the whole range. (ε,m)-Anonymity remedies the drawback of (k,e)-anonymity, that is, the ignorance of the distribution of sensitive values within the group.
δ-Presence was proposed by Nergiz et al. (2007) in considering a practical problem: The risk is simply from identifying that an individual is (or is not) in an anonymized database. The idea is that anonymizing such a database should mean that a recipient of the database should not be able to identify any individual as being in that database with certainty greater than δ.
ε-Differential privacy was proposed by Dwork (2006) in observing that there is no reasonable mechanism to protect certain type of privacy (impossibility result) because of the external (auxiliary) information. For example, given a statistical database of individuals’ heights and auxiliary information which states that Alice is 2 inch taller than average height, no matter Alice’s height is in the database or not there is no way to prevent revealing Alice’s absolute height other than control of the access of the database. Therefore, this principle requires that the participation of an object in the database should have no significant difference on the query answers. Given a database X with a domain D and a query (aggregate function) f with a Range (f), for any two instances A and B of X that differ only by any row x, the difference between the probability for a query answer S in Range (f) to be derived from A and that from B should be less than ε, i.e., Pr [K(f (A)) = S]/Pr [K (f (B)) = S]≤eε≈ 1 + ε, where K is a randomization operator.
ANONYMIZATION TECHNIQUES
Anonymization refers to the PPDP approaches that aim to hide the identity and sensitive information of individuals by transforming data to observe a particular privacy principle. Anonymization techniques can be broadly categorized as generalization and suppression and perturbation.
Generalization and suppression techniques: Generalization involves replacing specific values with a more general one. Suppression involves deleting values or records. Value suppression can be deemed as generalizing a value to unknown value *. LeFevre et al. (2005) categorizes generalization models into two classes. The first class is hierarchy-based models which use fixed value generalization hierarchies and are more suitable for categorical data. The second class is partition-based models which require the domain of an attribute to be a totally ordered set, define generalizations by partitioning the set into disjoint ranges and are most suitable for numerical data. Generalization models can also be categorized as follows.
Full domain generalization proposed by Samarati and Sweeney (1998) requires that all generalized values of an attribute in the anonymized data must be on the same level of the taxonomy tree of the attribute’s domain.
Full subtree generalization proposed by Iyengar (2002) requires that the child values sharing a common parent value are either all or none generalized and each generalization is applied to all records. This technique is more flexible than the full domain generalization.
Single-dimension partitioning proposed by Iyengar (2002) as well as Bayardo and Agrawal (2005) generalizes values of an attribute that has a total order by partitioning the values of the attribute into intervals independent of other attributes.
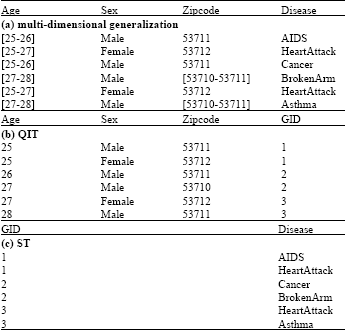
Multi-dimensional generalization proposed by LeFevre et al. (2006) allows a generalization step to be locally applied to a multi-dimensional region. e.g., data in Table 2 are full subtree generalization of data in Table 1a, data in Table 3a are multi-dimensional generalization of data in Table 1a. This technique incurs a smaller information loss than the full subtree generalization model but destroys domain exclusiveness in the generalized data.
Bucketization proposed by Xiao and Tao (2006a) publishes the exact quasi-identifier values and sensitive values in two separate tables QIT and ST and maintains the grouping information by a common attribute GID. Such a method limits the associations among quasi-identifier values and sensitive values. The drawback is that the adversary could easily confirm the participation of a target individual which is a privacy breach in some cases (Nergiz et al., 2007). Table 3b and c is a bucketization of data in Table 1a.
Perturbation techniques: While generalization and suppression retain data semantics at the record level, perturbation techniques retain data semantics at the aggregate level. Perturbation techniques usually are based on randomizations.
Permutation was employed by Zhang et al. (2007) to randomly permute the association between the quasi-identifier and the sensitive attribute to enforce (k,e)-anonymity.
| Table 3: | Multi-dimensional generalization and bucketization |
 | |
Additive random noise with uniform and Gaussian distribution was employed by Agrawal and Srikant (2000) to perturb numerical data. Additive random noise with a Laplace (0, σ) distribution was employed by Dwork (2006) to enforce differential privacy with σ being the sensitivity of the query answer to the presence/absence of any record.
Randomized response was employed by Du and Zhan (2003) to disguise binary data. The idea is to negate all values in a record by a certain probability which was extended by Huang and Du (2008) to disguise categorical data.
DATA UTILITY METRICS
An important objective of PPDP is to retain as much data utility as possible while observing a privacy principle. A data utility metric can be used in guiding anonymization algorithms and in evaluating the usefulness of anonymized data. There are general-purpose metrics as well as application-specific metrics. General-purpose metrics capture the notion to keep the data as specific as possible.
Generalization height was employed by Samarati and Sweeney (1998) to measure the information loss. It is the height of an anonymized data in the generalization lattice, i.e., the number of generalization steps that were performed.
Loss metric (LM) was presented by Iyengar (2002) to quantify the information loss by the ambiguity in generalizing a value which depends on how many other value cannot be distinguished from it. When generalizing values on a categorical attribute ACat in an indistinguishable group G into a generalized value ![]() , we have:
, we have:
where, ![]() is the information loss for each value on Acat in G, #leaves (Acat) is the number of leaves on the taxonomy tree associated with attribute Acat, and leaves (
is the information loss for each value on Acat in G, #leaves (Acat) is the number of leaves on the taxonomy tree associated with attribute Acat, and leaves ( ![]() ) is the number of leaves on the subtree rooted at
) is the number of leaves on the subtree rooted at ![]() . When generalizing values on numerical attribute ANum in an indistinguishable group G into an interval
. When generalizing values on numerical attribute ANum in an indistinguishable group G into an interval ![]() , we have:
, we have:
where, ![]() is the information loss for each value on ANum in G and |ANum| is the width of the domain of ANum. Xu et al. (2006) proposed NCP and Ghinita et al. (2007) proposed GCP, Liu and Wang (2010a) proposed bLM, that are variants of LM.
is the information loss for each value on ANum in G and |ANum| is the width of the domain of ANum. Xu et al. (2006) proposed NCP and Ghinita et al. (2007) proposed GCP, Liu and Wang (2010a) proposed bLM, that are variants of LM.
Classification Metric (CM) was presented by Iyengar (2002) to optimize the anonymized data for training a classifier, where each record is associated with a class label. CM assigns no penalty to an unsuppressed record that belongs to the majority class in its indistinguishable group. If a record is suppressed or it belongs to minority classes, it is penalized by 1.
Discernibility Metric (DM) was proposed by Bayardo and Agrawal (2005) which captures the desire to maintain discernibility between records. DM assigns each retained record a penalty equal to the size of the indistinguishable group the record belongs to, and each suppressed record a penalty equal to the size of the whole dataset.
KL-divergence was proposed by Kifer and Gehrke (2006) and employed by Ghinita et al. (2007) to compare two distributions F1 and F2 which can be used in evaluating the quality of an anonymized data. Let pi(k) be the probability of xi by Fk, KL-divergence is defined as follows which is minimized when F1 = F2:
Application-specific metrics capture the usefulness of the anonymized data in fulfilling a specific data mining task which is usually expressed as the accuracy of the data mining model built on the anonymized data and is only used in evaluating the quality of the anonymized data, rather than in guiding algorithms.
Classification error, defined as the gap between the prediction error of the classifier built on the anonymized data and that on the raw data, was used by Aggarwal and Yu (2004), Wang et al. (2004), Wang et al. (2005), Fung et al. (2005) and Wang and Fung (2006) to measure data utility.
Recall and precision of frequent patterns were proposed by Liu (2010) and Liu and Wang (2010a) to measure data utility in terms of the percentage of frequent patterns retained in the anonymized data and the precision of supports of the frequent patterns.
Average relative error in answering aggregate queries for a given query workload was used by LeFevre et al. (2006) and Xiao and Tao (2006a, b) to measure data utility which compares the estimated result on the anonymized data and the actual result on the original data.
ALGORITHMS
An algorithm transforms raw data by an anonymization technique to enforce a privacy principle and to retain as much information as possible in terms of a data utility metric.
Optimal search algorithms: Incognito proposed by LeFevre et al. (2005) generates the set of all k-anonymous full-domain generalizations with an optional record suppression threshold. Incognito makes use of the bottom-up aggregate computation technique and the a priori pruning. Incognito performed up to an order of magnitude faster than counterparts, such as Binary Search (Samarati, 2001) and MinGen (Sweeney 2002). Incognito was also adopted in finding full domain generalizations that observe l-diversity by Machanavajjhala et al. (2006) and t-closeness by Li et al. (2007).
k-Optimize proposed by Bayardo and Agrawal (2005) is the first practical algorithm that finds an optimal k-anonymization with the partition-based single dimension recording with suppression which exploits the monotonicity of k-anonymity and is suitable for attributes whose domains have a total order.
l+-Optimize by Liu and Wang (2010b) and OTA by Liu (2011) are the first optimal full subtree generalization algorithms that enforce l-diversity on relational data and transactional data, respectively. l+-Optimize and OTA improve efficiency by employing strong pruning based on information loss lower bounding and a novel enumeration strategy, respectively.
Anatomy proposed by Xiao and Tao (2006a) finds a bucketization in linear time which is optimal in the sense of minimizing the error of reconstructing the probability density function of records. Ghinita et al. (2007) improved Anatomy for a special case of one dimension quasi-identifier (only one attribute) by taking into account the quasi identifier values when grouping records.
Heuristic search algorithms: Mondrian proposed by LeFevre et al. (2006) is a greedy algorithm of multi-dimension partitioning for achieving k-anonymity. Mondrian takes the whole data as a multi-dimensional region and keeps on splitting any region R into two regions if R contains more than 2k records until all existing regions have a size ≤2k-1. Ghinita et al. (2007) extended their optimal single dimension bucketization algorithm to the multi-dimensional case by using space-mapping techniques such as Hilbert space filling curve.
TDS proposed by Fung et al. (2005) is a well known, greedily algorithm that finds a generalization solution by top-down, greedy search guided by a goodness metric that measures the trade-off between the gain of information and loss of anonymity. Similar algorithms were proposed by Wang et al. (2004) and Xiao and Tao (2006b) and so on.
mHgHs proposed by Liu and Wang (2010c) is a greedy algorithm that integrates full subtree generalization and suppression to enhance data utility. A multi-round, top-down greedy search approach was employed to ensure the performance in anonymizing high dimensional and large datasets.
Approximation and other algorithms: O(klogk)-approximation presented by Meyerson and Williams (2004) finds an approximation for the optimal problem of minimizing the diameter sum of hamming balls enclosing indistinguishable groups. O(k)-approximation presented by Aggarwal et al. (2005) is another approximation for the optimal k-anonymity problem.
r-Gather proposed by Aggarwal et al. (2006) is a constant-factor approximate clustering algorithm that is of general purpose and independent of the size of clusters which can be applied in producing k-anonymizations. Liu and Wang (2010a) proposed a clustering algorithm for k-anonymity based on semantic similarities.
Genetic algorithm was employed by Iyengar (2002) for finding a k-anonymous full subtree generalization. Multi-objective optimization was introduced by Huang and Du (2008) to find optimal disguise matrices for the randomized response technique.
CHALLENGES AND FUTURE DIRECTIONS
PPDP is quite challenging as the legitimate data recipient is a privacy adversary which results in the hardness to reach the optimal balance between privacy and data utility. Therefore, several questions remain open: can an optimal solution with a flexible anonymization model gain utility significantly; can a customized privacy principle improve utility; is it practical to find an optimal solution efficiently for real world data? In addition to these challenges, we identify the following future research directions.
PPDP for new data sharing forms and new data types: New privacy problems are ever emerging with new forms of information sharing, e.g., cloud computing and its implications for the privacy of personal information and for the confidentiality of business information, privacy issues in location-based services, privacy protection in social networks and privacy issues in sharing web search data.
PPDP integrated with information security technology: The ever-lasting challenge with privacy preserving data publishing is that privacy and utility are two contradicting goals. In many cases, it is hard to find a solution that provides sufficient privacy protection and retains enough data utility. Integrating privacy protection techniques with information security techniques could be a promising approach.
PPDP with social and legal issues: Privacy protection is a complicated social and psychological issue that cannot be fully addressed by technical solutions and need to be studied from multiple perspectives. Inter-disciplinary collaborative research is critical for providing real world privacy protection scenarios.
This study was supported in part by Zhejiang Natural Science Foundation (No.Y105700) and the Science and Technology Development Plan of Zhejiang Province (No. 2006C221034).