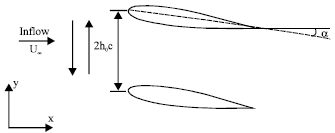
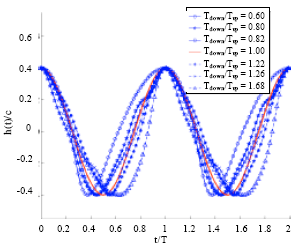
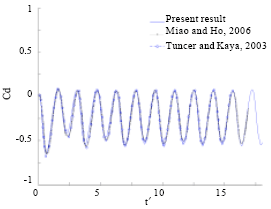
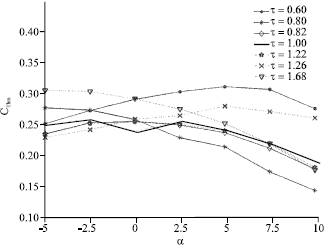
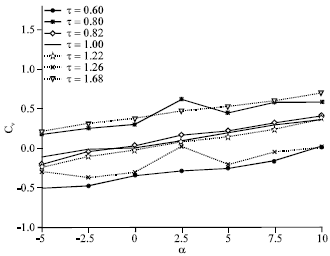
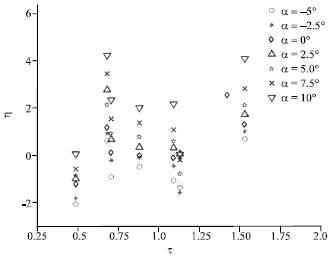
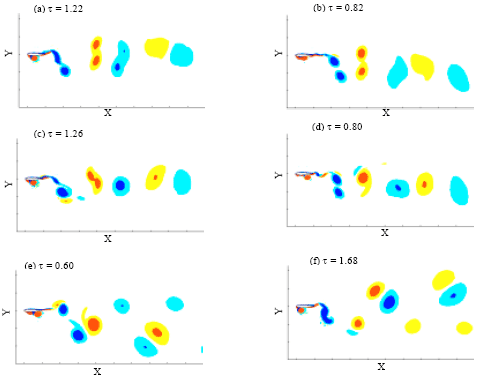
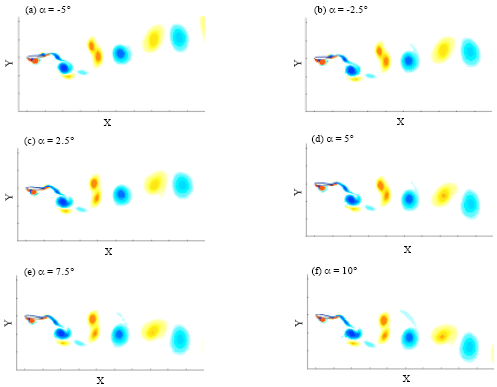
Research Article
Numerical Investigation on the Aerodynamic Characteristics of a Forward Flight Flapping Airfoil with Nonsymmetrical Plunging Motion
Department of Mechanical Engineering and Automation, Shenzhen Graduate School, Harbin Institute of Technology, Xili Shenzhen University Town, Shenzhen 518055, China
Zhou Chaoying
Department of Mechanical Engineering and Automation, Shenzhen Graduate School, Harbin Institute of Technology, Xili Shenzhen University Town, Shenzhen 518055, China