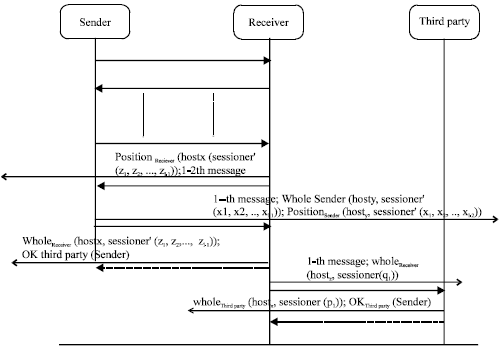
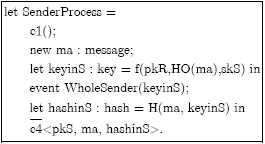
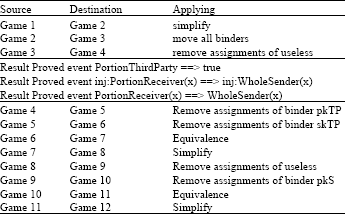
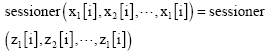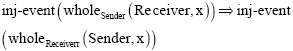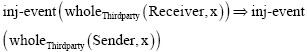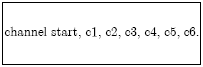Research Article
Automatic Verification of Deniable Authentication Protocol in a Probabilistic Polynomial Calculus with Cryptoverif
School of Computer, South-Center University for Nationalities, MinYuan Road #708, HongShan Section, Wuhan, Hubei 430074, China