Research Article
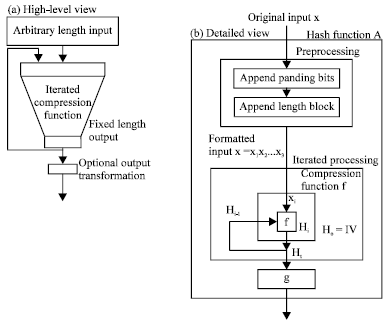
Encryption Algorithm of RSH (Round Sheep Hash)
Department of Information Management, Hunan University of Finance and Economics, No. 139, Fenglin 2nd Road, Changsha 410205, China
Yang Zhou
Department of Information Management, Hunan University of Finance and Economics, No. 139, Fenglin 2nd Road, Changsha 410205, China
Yunhua Xiao
Department of Information Management, Hunan University of Finance and Economics, No. 139, Fenglin 2nd Road, Changsha 410205, China
Guang Sun
Department of Information Management, Hunan University of Finance and Economics, No. 139, Fenglin 2nd Road, Changsha 410205, China