Research Article
An Improved Water-filling Power Allocation Method in MIMO OFDM Systems
College of Information Science and Engineering, Xinjiang University, Urumqi, XinJiang, People�s Republic China
The wireless communication system (Yang, 2005) coupled with multiple transmit/receive antennas and Orthogonal Frequency-Division Multiplexing (OFDM), is regarded as a promising solution for enhancing the data rates of next-generation wireless communication systems operating in frequency-selective fading environments. Recent research result shows that Multiple-Input and Multiple-Output (MIMO) techniques (Nanda et al., 2005) could be used to increase the capacity by a factor of the minimum number of transmit and receive antennas compared with a Single-Input Single-Output (SISO) system with flat fading or narrowband channels, while OFDM (Van Zelst and Schenk, 2004) can increase diversity gain and mitigate inter-symbol interference on a time-varying multi-path fading channel.
Furthermore, when channel parameters are known at the transmitter, the capacity of MIMO OFDM systems can be further increased by adaptively assigning transmitted power to orthogonal eigenmodes according to the water-filling rule (Telatar, 1999). At transmitters, the transmitted signals of different carriers are usually eigenbeamformed independently to orthogonal modes of spatial channels at every sub-channel in MIMO OFDM systems (Willink, 2005b; Stuber et al., 2004), which can be formed via spatial filtering according to the Singular Value Decomposition (SVD) of channel matrix at transmitters. However, these eigenmodes can not be used to steer the data symbols encoded by space-time codes, as one space-time codeword is transferred simultaneously by multiple carriers, while the eigenmodes are obtained at every carriers. So, when coupled with adaptive power and bit allocation, these eigenmodes have many disadvantages relative to their counterparts of a MIMO system in single-carrier transmission. Firstly, these eigenmodes ignore the effects of space-time diversity gains on the equivalent Signal Noise Ratios (SNR) of data symbols encoded by a space-time coder. Secondly, for a MIMO OFDM system configured with low rate space-time codes, it will be difficult to conduct adaptive power allocation as a large number of eigenmodes exist, compared with data symbols carried by one MIMO OFDM symbol. Thirdly, as one space-time codeword is carried by many eigenmodes at multiple carriers, it is also difficult to determine the modulation order of data symbols encoded in a space-time codeword. Therefore, these eigenmodes can be viewed as the simple generalization of their counterparts of a MIMO system in single-carrier transmission for conveniently analyzing system capacity, but not reflect the fact of one space-time codeword being carried by multiple sub-channels. Here, we present a new approach of constructing orthogonal eigenmodes in MIMO OFDM systems. For a MIMO OFDM system with least-squared decoders, orthogonal eigenmodes can be obtained by the SVD of equivalent channel matrix in system models, where a general space-time code is considered in a general view. The result eigenmodes are correspondent to data symbols encoded in space-time codewords carried by one MIMO OFDM symbol. Thus, the novel eigenmodes can be used directly to steer adaptive power allocation to data symbols and their bit allocations, as usually do in a MIMO system with single-carrier transmission.
Subsequently, based on novel eigenmodes, an improved water-filing power allocation scheme is also proposed to determine the power allocation and its correspondent bit number for reason of complexity or poor performance of existing schemes. The classical water-filing power allocation scheme (Telatar, 1999) is only optimal to maximize system capacity but with a great deal of residual power by reason of discrete modulation orders. Hence, many improved water-filling schemes (Ren et al., 2004; Van den Bogaert et al., 2004; Liang et al., 2003) or other power allocation schemes (Shi et al., 2004; Codreanu et al., 2005; Quoting et al., 2005; Ng et al., 2002) are given in recent research literatures, such as iterative water-filing algorithms (Van den Bogaert et al., 2004), sub-channel group water-filling scheme (Liang et al., 2003), greedy algorithms (Codreanu et al., 2005), iterative bits power allocation (Quoting et al., 2005), and so on. Among these schemes, only greedy power allocation is optimal to maximize the transported total bits but at a cost of calculation overhead. Moreover, similar to greedy algorithm, other schemes are conducted in iterative wise, and their convergences have significant effects on system performance. Whereas, the improved water-filling power allocation scheme can be done in two steps and can also achieve the maximized transported bits. According to the scheme, the classical water-filling strategy is firstly adopted to determine the optimal power allocation and corresponding bit number for every eignmode, followed by a residual power reallocation to further determine additional bit number carried by those eigenmodes.
The MIMO OFDM system Model with universal space-time codes: Firstly, a universal space-time code can be defined as a rate T/K MxK design scheme over a complex subfield A of the complex field C, whose codeword matrix X is a MxK matrix with entries obtained from the K-linear combinations of T data symbols and their conjugates. If a codeword matrix X is represented as a column vector by stacking its columns, the column vector can be delineated as the linear transform of T data symbols and their conjugates, i.e:
| (1) |
where, vec(.) denotes the column vector by stacking the columns of a matrix into one column vector, s is a column vector whose elements consist of T data symbols and their conjugates, and the transform matrix Φ is denoted as the generation matrix of the space-time code design scheme.
Then, let us consider a MIMO OFDM system with M transmit and N receive antennas, and an OFDM modulation is conducted on K sub-carriers, as illustrated in Fig. 1. A space time code is used to encode a data symbol vector s along space-time directions with T data symbols and their conjugates, while a least squared space-time decoder is used to restore the transmitted data symbols by decoding the received space-time signals. In order to delineate the system model compactly, we omit the time indicator of MIMO OFDM symbols and neglect symbol timing errors and frequency offsets. Assume a MIMO OFDM only can carry one space-time codeword, so the receive signals in a MIMO OFDM symbol period can be given as:
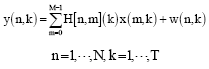 | (2) |
where, y (n,k) is the received data at the k-th carrier of the nth receive antenna, H (n,m)(k) represents the fading coefficient at the kth carrier of the spatial channel between the nth receive antenna and the mth transmit antenna, x (m,k) denotes the element at mth row and kth column of a space-time codeword matrix X, and w (n,k) is the channel noise at the k-th carrier for the n-th receive antenna.
Substituting the sum term in Eq. 2 by its matrix form, we rewrite Eq. 2 as:
| (3) |
where, x (:, k) is the k-th column of space-time codeword X, H[n,:] (k) is the n-th column of the MIMO channel fading coefficient matrix H(k) at k-th carriers, which can be delineated as:
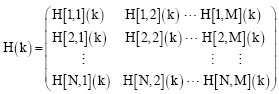 | (4) |
Let y(n,:) denote the received signal vector at the n-th receive antenna in a MIMO OFDM symbol period, we can rewrite (3) into matrix form as:
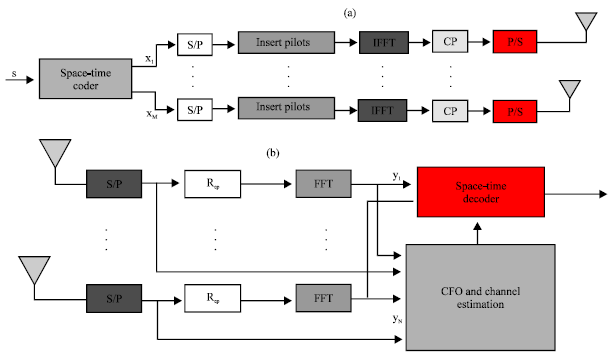 | |
| Fig. 1: | Discrete-time equivalent base-band model of a MIMO OFDM block transmission system. (a) Transmitter and (b) Receiver |
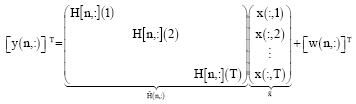 | (5) |
where, w(n,:) is the channel white noise corresponding to y(n,:), and ![]() . Thus, in a MIMO OFDM symbol period, assembling the received signals from all the receive antennas into a matrix form, we can get:
. Thus, in a MIMO OFDM symbol period, assembling the received signals from all the receive antennas into a matrix form, we can get:
| (6) |
where:
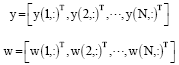 |
and ![]() is given by:
is given by:
According to Eq. 6, the least squared estimation of s can be achieved as following:
| (7) |
where:
Then, since s consists of T data symbols and their conjugates, the transmitted data can be derived from ![]() , completely. Moreover, for the scenario where a MIMO OFDM symbol can carry multiple space-time codewords, the similar results can also be derived in the same way.
, completely. Moreover, for the scenario where a MIMO OFDM symbol can carry multiple space-time codewords, the similar results can also be derived in the same way.
A novel eignmode transmission coupled with space time codes: By singular value decomposition, the eigenmodes concealed in Eq. 6, can be disclosed in the same way as their counterparts in single-carrier M IMO systems (Ng et al., 2002). Let ![]() , it can be decomposed into orthogonal eigenmodes by singular value decomposition as showed:
, it can be decomposed into orthogonal eigenmodes by singular value decomposition as showed:
| (8) |
where, U and V denote the unitary matrices representing the left and right eigenvectors of ![]() , respectively, and D is a diagonal matrix, whose elements are the ordered singular values of
, respectively, and D is a diagonal matrix, whose elements are the ordered singular values of ![]() , i.e., the corresponding fading coefficients of those orthogonal eigenmodes.
, i.e., the corresponding fading coefficients of those orthogonal eigenmodes.
Then, according to Eq. 6 and 8, substituting ![]() by its SVD, we can get:
by its SVD, we can get:
| (9) |
Now, let , ![]() ,
, ![]() ,
, ![]() and Eq. 9 can be rewritten as:
and Eq. 9 can be rewritten as:
| (10) |
Furthermore, it is also equivalent to:
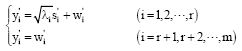 | (11) |
where, r and ![]() are the rank of
are the rank of ![]() and its i-th singular value, respectively.
and its i-th singular value, respectively.
As the equivalent channel matrix ![]() includes the generation matrix of space-time codes, the eigenmodes obtained by Eq.10 can also reflect the corresponding space-time diversity gains of space-time codes. Furthermore, these eigenmodes have unique corresponding relations with the data symbols, transported by one MIMO OFDM symbol. Thus, according to these eigenmodes and power allocation schemes, it’s very easy to determine the modulation orders of these data symbols and their transmit power. So, when compared with the classical eigenmodes for different carriers as showed in reference (Nanda et al., 2005; Willink, 2005a; Stuber et al., 2004), adaptive spatial processing could be performed conveniently with these novel eigenmodes.
includes the generation matrix of space-time codes, the eigenmodes obtained by Eq.10 can also reflect the corresponding space-time diversity gains of space-time codes. Furthermore, these eigenmodes have unique corresponding relations with the data symbols, transported by one MIMO OFDM symbol. Thus, according to these eigenmodes and power allocation schemes, it’s very easy to determine the modulation orders of these data symbols and their transmit power. So, when compared with the classical eigenmodes for different carriers as showed in reference (Nanda et al., 2005; Willink, 2005a; Stuber et al., 2004), adaptive spatial processing could be performed conveniently with these novel eigenmodes.
Furthermore, as the relations between the equivalent channel matrix and the generation matrix of one space-time code, system capacity is significantly effected on by the code rate of space-time codes. For one space-time code scheme with a unitary generation matrix, the space-time diversity doesn’t change the corresponding system capacities without space-time codes. That is, the number of data symbols in the novel eigenmodes should be identical to that in classical eigenmodes. So, there exists M=2*T/K for space-time codes that could keep system capacity unchanged, and only Alamouti space-time code exists for a transmitter with two antennas, when T/K is not more than one. For other space-time codes, system capacity will increase in inverse proportion to space-time code rates, i.e., the larger the transmission rate, the more the system capacity. In section V, this will be disclosed by numerical simulation results.
Generally speaking, the classical eigenmodes at different carriers for MIMO OFDM systems can be viewed as simple extensions of the eigenmodes in MIMO systems in single-carrier transmission, which fit for the analysis of system capacity other than link adaptation techniques. However, besides system capacity analysis, the novel eignmode transmission can couple space-time codes and link adaptation techniques, perfectly. Furthermore, the number of novel eigenmodes is only limited to the number of the transmitted data symbols carried by a MIMO OFDM symbol, while M*M eigenmodes have to be disclosed to conduct power allocation to data symbols transported in these eigenmodes.
Improved water-filling power allocation algorithm: Based on adaptive modulation margin adaptive (MA) principals, link adaptation techniques can be implemented from two aspects, i.e., adaptive power allocation under total transmit power constraint for maximal transported bits, and adaptive bits allocation under total transmit bits for minimal transmit power, respectively. In this study, under the constraints of given total power and target Bit Error Ratio (BER), we only consider how to conduct power allocation to orthogonal eigenmodes in order to maximize transmit bits.
For given target BER Pe, the transmit power for an additive white Gaussian noise (AWGN) channel to transmit c bits information with M-QAM modulation, is given by Codreanu et al. (2005):
| (12) |
where:
is denoted as complementary error function. Then, for given transmit power, the number of bits transported by the AWGN channel, can be derived according to Eq. 12, as showen in the following formula:
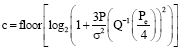 | (13) |
where, floor denotes the operator to round towards minus infinity.
In order to maximize the transported total bits, a improved water-filling power allocation scheme is given on the base of classical water-filling schemes. According to the scheme, the adaptive power and bit allocation are conducted in two steps. Firstly, an initial power allocation is given by classical water-filling scheme, That is, the first step is executed to initially allocate the power for different orthogonal eigenmodes according to the classical water-filling scheme. Then, after determining the transported bits at channel eigenmodes, the residual power is reallocated among these eigenmodes to transport additional bits. Now, the following, we present the details of the improved water-filling scheme, which is also illustrated its flow chart as showen in Fig. 2.
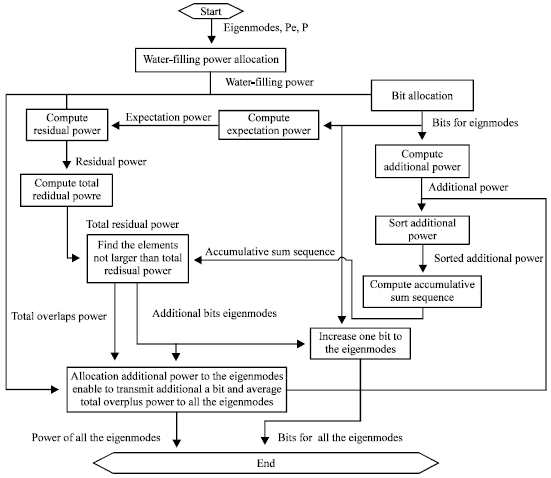 | |
| Fig. 2: | Flow chart for the improved water-filling power algorithm |
Initial power allocation based water-filling scheme: For the eigenmodes given by Eq. 11, the power allocation scheme can be described as an optimal problem to maximize the system capacity under the constraint of given total transmit power, i.e:
| (14) |
where, C denotes system capacity, while P is the given total transmit power. According to water-filling power allocation algorithm, the optimal power allocation can be given by:
| (15) |
where:
and σ2 is noise variance of orthogonal eigenmodes, assumed to have the same variance.
The power allocated to orthogonal eigenmodes as showen in Eq. 15, is called water-filling power to distinguish different power allocation results in the following. With the water-filling power allocated the ith eignmode, its maximal bits carried can be given by Eq. 13, that is:
| (16) |
However, according to Eq. 12, the necessary power to transmit ci bits is determined by:
| (17) |
which is called the expectation power to transmit ci bits. Clearly, the water-filling power for the i-th eignmode is larger than its expectation power, and their difference is named as residual power, which will be further reallocated among these eigenmodes.
Reallocation of residual power: Subsequently, on the basis of the power allocation results in the first period, we calculate the additional power to transmit an additional bit at the ith eignmode. That is:
| (18) |
which is called additional power. Then, an accumulative sum sequence is obtained by a sorted version of additional power in ascending order at all the eigenmodes. The elements in the accumulative sum sequence, not more than the total residual power, can be found out, and the eigenmodes corresponding with these elements can transport an additional bit. So, the additional powers of these eigenmodes are allocated to these eigenmodes from the total residual power, whose residual power after reallocation, i.e., total overplus power, is averagely allocated to all the eigenmodes. At last, the bit number of these eigenmodes should be increased by one, respectively.
It’s very clear that the improved scheme as presented above can improve the usage of power and transmit more bits than the classical water-filling power allocation scheme (Codreanu et al., 2005). Furthermore, its simple implementation also has smaller delay than the greedy algorithm. Hence, it is feasible for the MIMO OFDM systems with a larger number of carriers.
SIMULATION RESULTS
Here, we firstly consider a MIMO OFDM system with 2048 carriers at carrier frequency of 4.5 GHz, which has 20 MHz bandwidth and a 1/4 OFDM symbols as guard intervals, which can eliminate intersymbol interference (ISI) caused by frequency selective channels. Under spatially uncorrelated ITU vehicular A channels (Ng et al., 2002) with Doppler frequencies of 200 Hz, we evaluate the system capacities and throughputs with and without considering space-time codes, respectively. By the reason of terseness, the eigenmodes obtained for the two scenarios are called space-time eigenmodes and carrier eigenmodes, respectively. At transmitter, the water-filling power allocation algorithm (Telatar, 1999) is executed to adaptively adjust the transmit powers for all the eigenmodes according to their fading coefficients.
Figure 3 shows the system capacities for different signal noise ratios (SNR) when space-time codes are Alamouti Code, Space-Time Block Code (STBC) ![]() (Ng et al., 2002) and STBC
(Ng et al., 2002) and STBC ![]() (Ng et al., 2002) with code rates of 1, 0.5 and 0.75, respectively. According to Fig. 3, the code rates of space time codes have significant effects on the system capacity when the space-time eigenmodes are constructed, i.e., the smaller the code rates, the larger the capacity difference between carrier eigenmodes and space-time eigenmodes. As the results pointed out in that, this phenomenon can owe to the increase of space-time diversity gains with the decrease of code rates, which lead to the reduction of data symbol transmit rates. At the same time, the scales of system capacities for the carrier eigenmodes and the space-time eigenmodes are evaluated by twenty time numerical simulation under the uncorrelated ITU indoor, pedestrian and vehicular A channel scenarios, respectively. Then, these scale factors are averaged out to 1.9526, 4.4807 and 3.5509, when Alamouti Code, Space-Time Block Code (STBC)
(Ng et al., 2002) with code rates of 1, 0.5 and 0.75, respectively. According to Fig. 3, the code rates of space time codes have significant effects on the system capacity when the space-time eigenmodes are constructed, i.e., the smaller the code rates, the larger the capacity difference between carrier eigenmodes and space-time eigenmodes. As the results pointed out in that, this phenomenon can owe to the increase of space-time diversity gains with the decrease of code rates, which lead to the reduction of data symbol transmit rates. At the same time, the scales of system capacities for the carrier eigenmodes and the space-time eigenmodes are evaluated by twenty time numerical simulation under the uncorrelated ITU indoor, pedestrian and vehicular A channel scenarios, respectively. Then, these scale factors are averaged out to 1.9526, 4.4807 and 3.5509, when Alamouti Code, Space-Time Block Code (STBC) ![]() (Ng et al., 2002) and STBC
(Ng et al., 2002) and STBC ![]() are considered, respectively. However, this doesn’t mean the throughputs of carrier eigenmodes are larger than that of space-time eigenmodes, as showed in the following simulation results.
are considered, respectively. However, this doesn’t mean the throughputs of carrier eigenmodes are larger than that of space-time eigenmodes, as showed in the following simulation results.
Furthermore, when space-time codes are Alamouti Code, Space-Time Block Code (STBC) ![]() and STBC
and STBC ![]() with code rates of 1, 0.5 and 0.75, respectively, the throughputs for different signal noise ratios (SNR) are given in Fig. 4, where the modulation order of data symbols in carrier eigenmodes is fixed unchanged in a space-time codeword. However, the adaptive modulation is only performed on the data symbols of space-time codes, for the case of space-time eigenmodes other than carrier eigenmodes, as the data symbols carried by space-time codes in carrier eigenmodes are transported by multiple carrier eigenmodes, simultaneously. Due to adaptive modulation of data symbols for space-time eigenmodes, the larger throughputs are achieved than that of carrier eigenmodes, as showed in Fig. 4, while the throughputs also increase with the code rate of space-time codes, at the SNR above 15 dB. What’s more, the ratios between the numbers of carrier eigenmodes and space-time eigenmodes are 1, 3 and 2 for Alamouti Code, Space-Time Block Code (STBC)
with code rates of 1, 0.5 and 0.75, respectively, the throughputs for different signal noise ratios (SNR) are given in Fig. 4, where the modulation order of data symbols in carrier eigenmodes is fixed unchanged in a space-time codeword. However, the adaptive modulation is only performed on the data symbols of space-time codes, for the case of space-time eigenmodes other than carrier eigenmodes, as the data symbols carried by space-time codes in carrier eigenmodes are transported by multiple carrier eigenmodes, simultaneously. Due to adaptive modulation of data symbols for space-time eigenmodes, the larger throughputs are achieved than that of carrier eigenmodes, as showed in Fig. 4, while the throughputs also increase with the code rate of space-time codes, at the SNR above 15 dB. What’s more, the ratios between the numbers of carrier eigenmodes and space-time eigenmodes are 1, 3 and 2 for Alamouti Code, Space-Time Block Code (STBC) ![]() and STBC
and STBC ![]() , respectively. Consequently, the link adaptation technique with a few eigenmodes can be implemented effectively in space-time eigenmodes.
, respectively. Consequently, the link adaptation technique with a few eigenmodes can be implemented effectively in space-time eigenmodes.
Subsequently, the improved water-filling power allocation scheme is tested in the same system configuration scenarios as showed above, while other power allocation algorithms such as classical water-filling scheme (Telatar, 1999) and greedy algorithm (Codreanu et al., 2005), are also evaluated as comparisons. Under given target BER 10-3, their throughput curves for the MIMO OFDM systems with two transmit antennas and four receive antennas, are showed in Fig. 5, where the Alamouti Space-Time Code is used to encode the transported data symbols in space-time domain for the case of space-time eigenmodes.
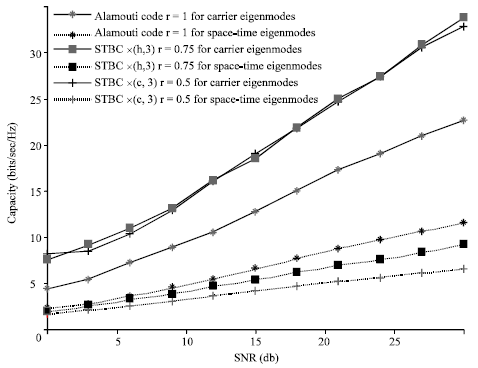 | |
| Fig. 3: | Capacity curves of the MIMO OFDM systems when the carrier eigenmodes and space-time eigenmodes are conducted for the space-time codes with different code rates |
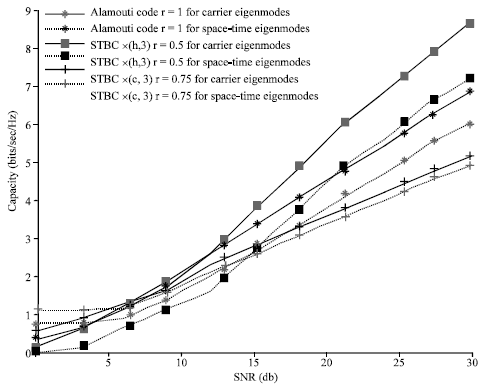 | |
| Fig. 4: | Throughput curves of MIMO OFDM systems when the carrier eigenmodes and space-time eigenmodes are conducted for the space-time codes with different code rates, where different powers are allocated to different eigenmodes according to water-filling scheme with given target BER 10-6 |
According to Fig. 5, the improved water-filling power allocation scheme can achieve good results than that the classical water-filling scheme achieves at SNR above 16 dB, as the power allocation strategy is introduced to obtain additional transported bits at a cost of sensibility to noise. However, the results in Fig. 5 also indicate the improved scheme is actually a sub-optimal scheme, whose performance is inferior to that of greedy algorithm.
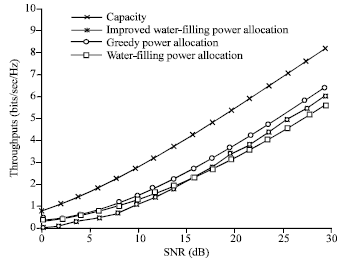 | |
| Fig. 5: | Throughputs of the MIMO OFDM system with Alamouti Space-Time Code when the space-time eigenmodes with water-filling, equal power, greedy and improved water-filling power allocation scheme are conducted with given target BER 10-6 |
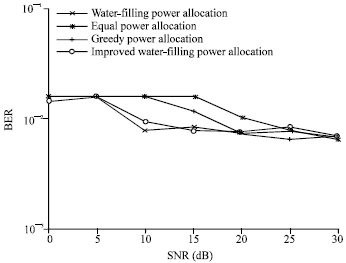 | |
| Fig. 6: | Bit error ratio (BER) of MIMO OFDM system with Alamouti Space-Time Code when space-time eigenmodes with water-filling, equal power, greedy and improved water-filling power allocation schemes are conducted with target BER 10-3 |
At last, for given target BER 10-3, the system average BER curves under different power allocation schemes, are showen in Fig. 6 for the MIMO OFDM systems with the same configuration as showed above, when the Alamouti Space-Time Code is adopted. As indicated in Fig. 6, the improved water-filling scheme can obtain better system BER performance than greedy algorithm and equal power schemes but inferior to classical water-filling scheme. Hence, the improved water-filling scheme can work as an alternative scheme of greedy scheme and water-filling algorithm.
For a MIMO OFDM system configured with least-squared space-time decoders, the proposed novel eignmode transmission with considering universal space-time codes can integrate generation matrix of space-time codes with spatial MIMO channel matrix. Compared with the classical eigenmodes at different carriers, these novel eigenmodes can be used to conduct transmit power allocation for those data symbols, as usually do in MIMO systems in single-carrier transmission. It would be more convenient to perform link adaptation technology with novel eignmode transmission than that with classical eigenmodes. Furthermore, the improved water-filling power allocation scheme given in this study could obtain comparable throughputs and system BER, when compared with greedy algorithm(Codreanu et al., 2005), the classical water-filing power allocation scheme (Telatar, 1999), iterative water-filing algorithms (Van den Bogaert et al., 2004), sub-channel group water-filling scheme (Liang et al., 2003), many improved water-filling schemes (Ren et al., 2004; Van den Bogaert et al., 2004; Liang et al., 2003), respectively.
In this study, an improved water-filling scheme is proposed for determining the optimal transmit powers for orthogonal eigenmodes. Results indicate that the improved water-filling scheme can obtain good tradeoff, with comparison to classical water-filling schemes and greedy algorithms respectively. Compared with classical water-filling scheme, it can also obtain larger throughputs via residual power allocation.