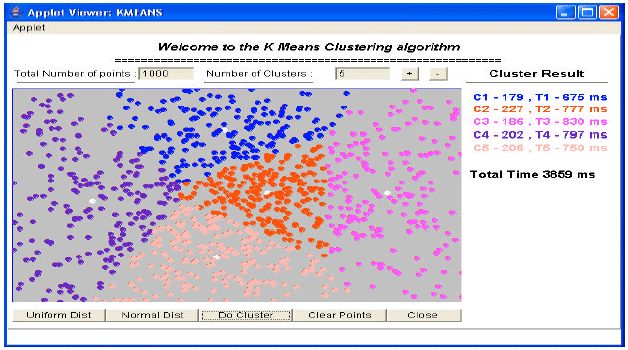
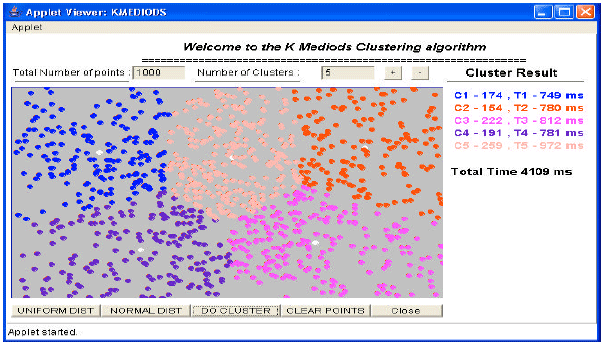
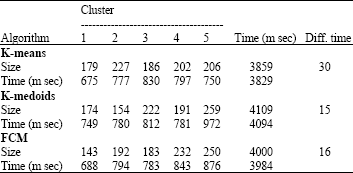
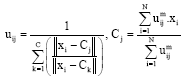Review Article
A Survey of Partition based Clustering Algorithms in Data Mining: An Experimental Approach
PG and Research Department of Computer Science, D.G. Vaishnav College, Chennai-600106, India
T. Santhanam
PG and Research Department of Computer Science, D.G. Vaishnav College, Chennai-600106, India