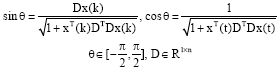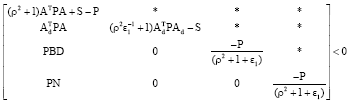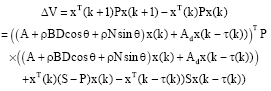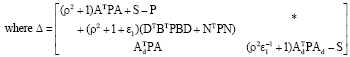Research Article
Stabilization for a Class of Time-delay Discrete Bilinear System
General Education Center, Fortune Institute of Technology, Kaohsiung County 83160, Taiwan, Republic of China
Ming-Ying Hsiao
Department of Electrical Engineering, Fortune Institute of Technology, Kaohsiung County 83160, Taiwan, Republic of China
Shun-Hung Tsai
Graduate Institute of Automation Technology, National Taipei University of Technology, Taipei 10608, Taiwan, Republic of China