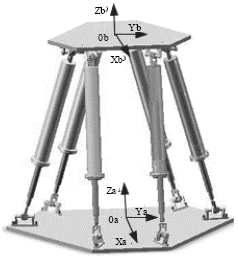
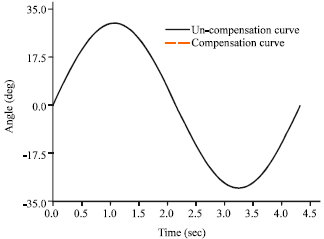
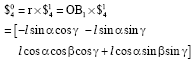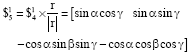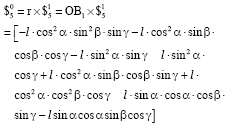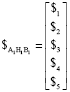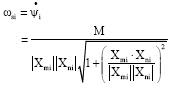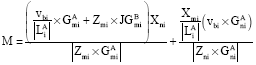Research Article
Simulation of 6-DOF Parallel Robot for Coupling Compensation Method
School of Mechanical Engineering, Dalian University of Technology, Dalian, China
Yingha Wu
School of Mechanical Engineering, Dalian University of Technology, Dalian, China
Dong Liu
School of Mechanical Engineering, Dalian University of Technology, Dalian, China
Yu Du
School of Mechanical Engineering, Dalian University of Technology, Dalian, China
Haiying Wen
School of Mechanical Engineering, Dalian University of Technology, Dalian, China
Junfa Yu
NO.65053 Army, Dalian, China