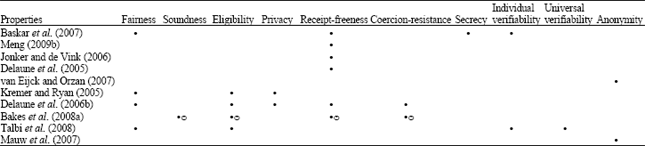
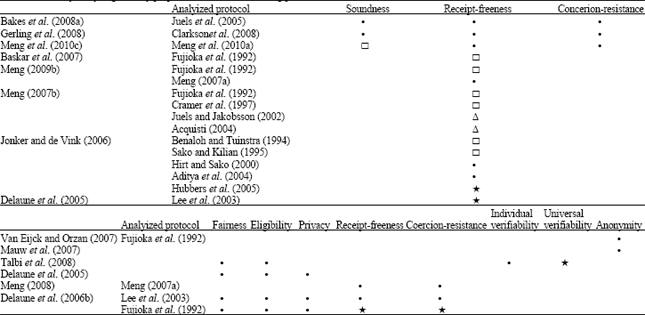
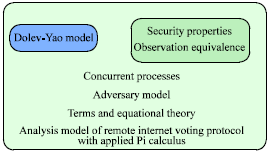
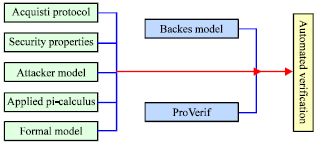
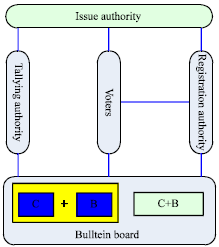
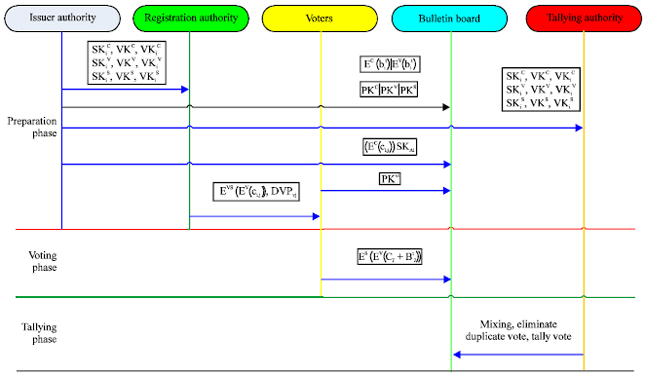
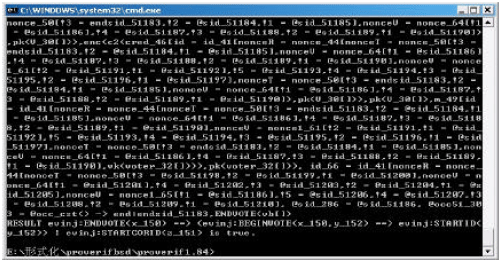
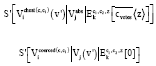Research Article
Refinement of Mechanized Proof of Security Properties of Remote Internet Voting Protocol in Applied PI Calculus with Proverif
School of Computer, South-Center University for Nationalities, MinYuan Road No. 708, HongShan Section, Wuhan, Hubei, 430074, China