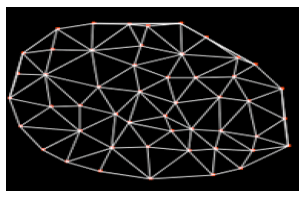
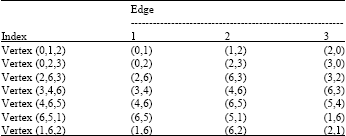
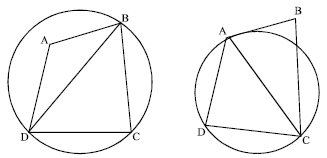
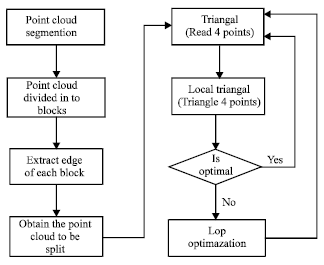
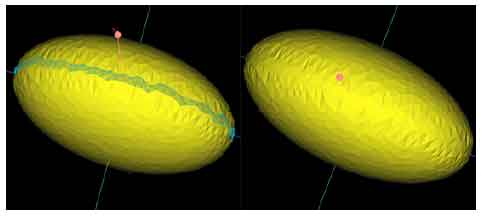
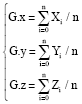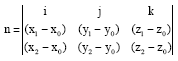Research Article
A New Rapid Triangulation Method of Space Closed Point Cloud
School of Information Engineering, Nanchang Hangkong University, Nanchang, People`s Republic of China
Linghong Zhu
School of Information Engineering, Nanchang Hangkong University, Nanchang, People`s Republic of China
Qinghui Xiao
School of Information Engineering, Nanchang Hangkong University, Nanchang, People`s Republic of China