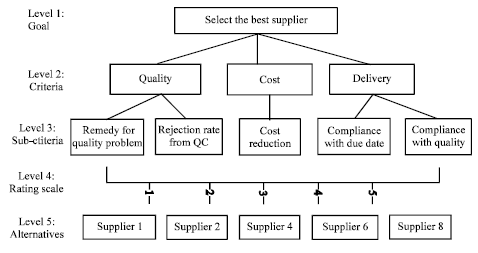
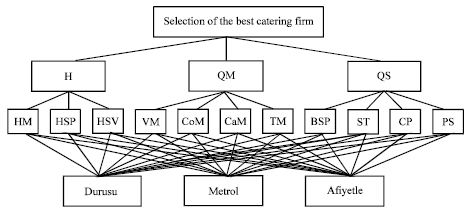
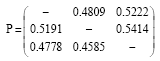Research Article
An Intuitionistic Fuzzy AHP Based on Synthesis of Eigenvectors and its Application
Department of Management Science and Engineering, Nanjing Normal University, Nanjing 210046, China
Gang Qian
Jiangsu Research Center of Information Security and Privacy Technology, Nanjing 210046, China
Xiangqian Feng
Department of Management Science and Engineering, Nanjing Normal University, Nanjing 210046, China