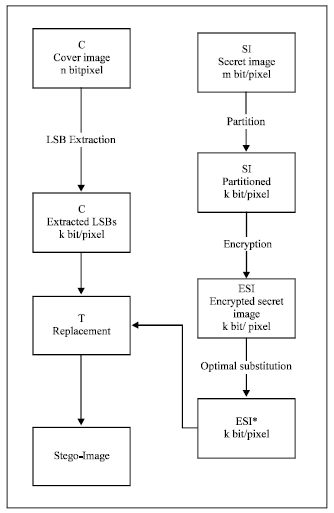
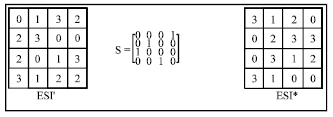
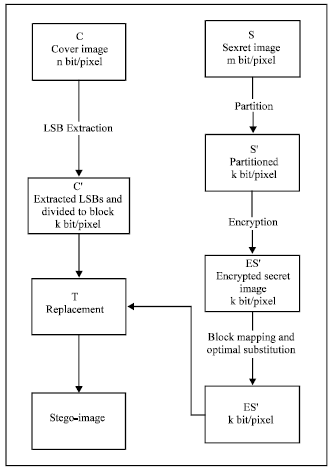
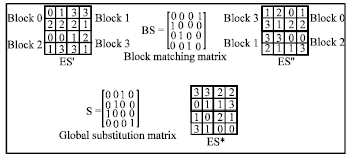
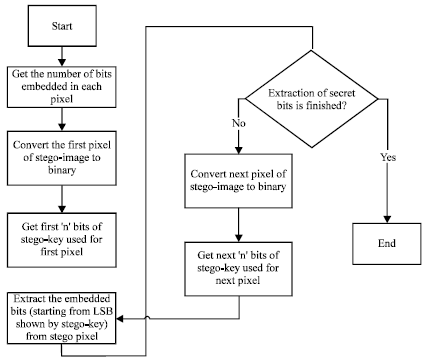
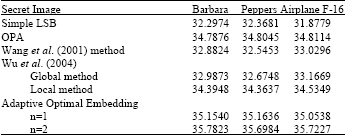
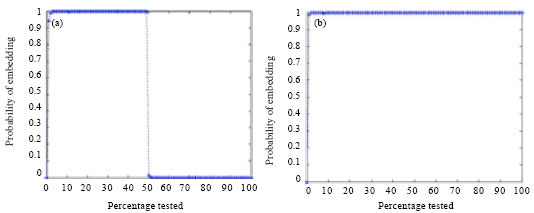
Research Article
Adaptive Image Steganography Based on Optimal Embedding and Robust Against Chi-square Attack
Faculty of Computer Science and Information Systems, Universiti Teknologi Malaysia, Malaysia
Subariah Ibrahim
Faculty of Computer Science and Information Systems, Universiti Teknologi Malaysia, Malaysia