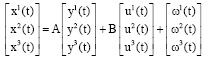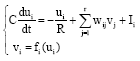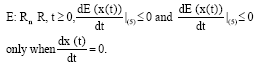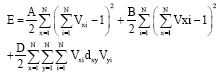Research Article
Energy Function Analysis and Optimized Computation Based on Hopfield Neural Network for Wireless Sensor Network
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan Hubei, 430074, China
Bingwen Wang
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan Hubei, 430074, China
Wei Wang
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan Hubei, 430074, China
Zhuo Liu
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan Hubei, 430074, China
Chao Gao
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan Hubei, 430074, China