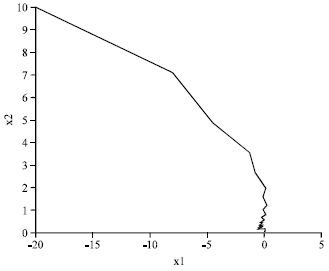
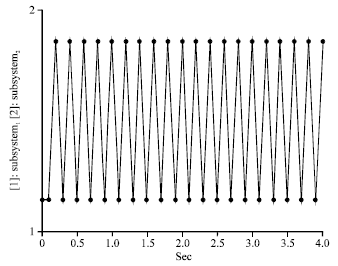
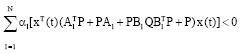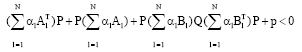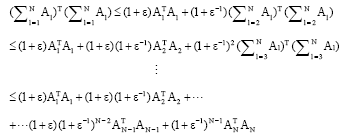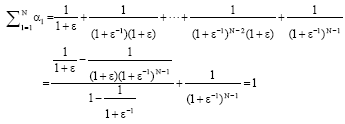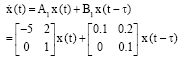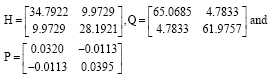Research Article
Delay Independence Stability Analysis and Switching Law Design for the Switched Time-delay Systems
Department of Electrical Engineering, Southern Taiwan University, No.1, NanTai Street, Yongkang District, Tainan City, Taiwan, Republic of China
Juing-Shian Chiou
Department of Electrical Engineering, Southern Taiwan University, No.1, NanTai Street, Yongkang District, Tainan City, Taiwan, Republic of China
Chun-Ming Cheng
Department of Electrical Engineering, Southern Taiwan University, No.1, NanTai Street, Yongkang District, Tainan City, Taiwan, Republic of China