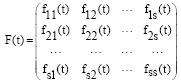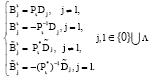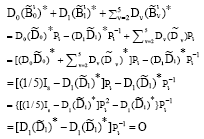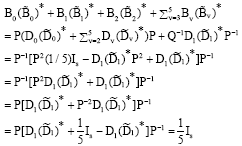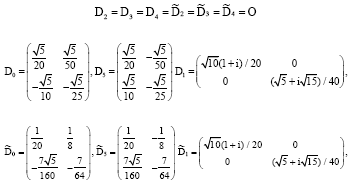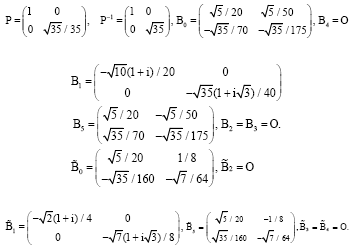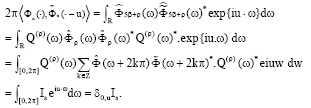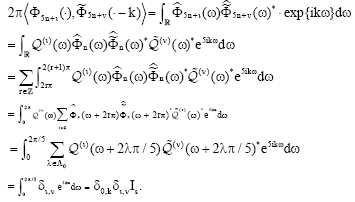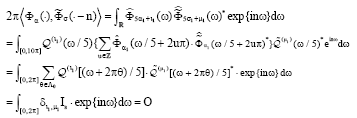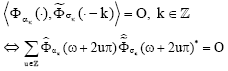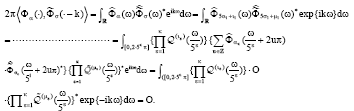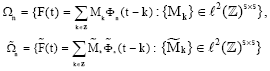Research Article
An Algorithm for Designing a Sort of Biorthogonal Multiple Vector-valued Wavelets and their Properties
School of Science, Xi`an University of Architecture and Technology, Xi`an 710055, Peoples Republic of China
Baoxian Lv
Department of Fundamentals, Henan Polytechnic Institute, Nanyang 473009, People�s Republic of China